基于季节性指数平滑法的学校因病缺课预测研究

顾蓉艳; 张玲; 宋肖肖; 李燕; 蔡乐; 崔文龙; 刘伟

doi:10.16462/j.cnki.zhjbkz.2019.07.020

基于季节性指数平滑法的学校因病缺课预测研究

doi: 10.16462/j.cnki.zhjbkz.2019.07.020

650500 昆明, 昆明医科大学公共卫生学院健康研究所

基金项目:

云南省边境地区症状监测预警防控体系研究与应用 214YNPHXT23

详细信息

通讯作者:
刘伟, E-mail: liuweikm@qq.com

中图分类号: R181
计量
- 文章访问数: 485
- HTML全文浏览量: 200
- PDF下载量: 44
- 被引次数: 0
出版历程
- 收稿日期: 2018-12-02
- 修回日期: 2019-03-22
- 刊出日期: 2019-07-10

Predictive study on school absences due to illness with seasonal exponential smoothing method

Department of Institute of health, School of public Health, Kunming Medical University, Kunming 650500, China

Funds:

Research and Application of Disease Monitoring and Early Warning System in Border Areas of Yunnan Province 214YNPHXT23

More Information

Corresponding author: LIU Wei, E-mail: liuweikm@qq.com

摘要

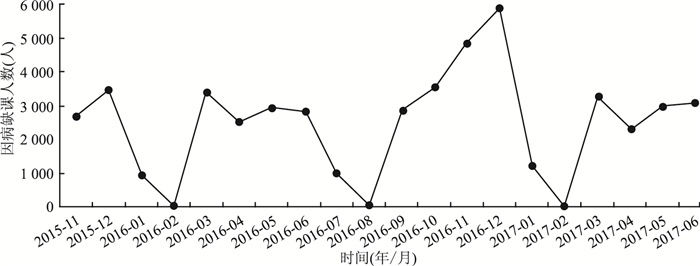
摘要: 目的建立适合学校因病缺课人数的指数平滑法预测模型，探讨该模型在学校因病缺课预测中的应用价值，为因病缺课在疾病预警中发挥作用提供依据。方法收集2015年11月-2017年6月云南南部边境县症状监测系统中的30所小学因病缺课人数数据，分别采用简单季节法、温特斯加法、温特斯乘法进行建模拟合，通过指标分析、统计量分析、残差图分析对3种模型进行全面比较，选出最佳模型，并预测3个月学校因病缺课情况。结果简单季节法、温特斯加法、温特斯乘法拟合因病缺课人数在时间序列上的变动趋势，均方根误差(root mean square error，RMSE)分别为445.11、420.99、258.75，调整决定系数R²分别为0.72、0.72和0.77，R²为0.92、0.93和0.98，Ljung-Box Q的概率为0.54、0.43和0.21；预测模型线性趋势Alpha分别为0.999、1.000、0.298；预测值与实际值平均相对误差分别为9.62%、21.90%和7.52%。结论温特斯乘法指数平滑法能够较好的对学校因病缺课情况进行预测预警，具有实用价值，可为早期识别异常信号提供科学依据。
- 指数平滑法 /
- 时间序列 /
- 学校因病缺课 /
- 预测
Abstract: Objective To establish a suitable exponential smoothing prediction model for school absentees due to illness, to discuss its application value for predicting school absences due to illness, and to provide a basis for early warning of absence due to illness. Methods Numbers of schools absences by year and month due to illness in 30 primary schools from November 2015 to June 2017 were collected from symptom monitoring system of border county, southern Yunnan and Simple seasonal model, Winters addition model and Winters multiplication model were used to build simulation. The data of July 2017 to December 2017 were used for model validation. The three models were overall compared and evaluated through indicator analysis, statistical analysis and residual diagram analysis. The best model was selected to predict school absences due to illness from January 2018 to March 2018. Results Simple seasonal model, Winters addition model and Winters multiplication model were used to fit the variation trend of number of school absences due to illness in time series. The root mean square error (RMSE) of three models were 445.11, 420.99 and 258.75; R_adj² were 0.72, 0.72 and 0.77; R² were 0.92, 0.93 and 0.98; P values of Ljung-Box Q were 0.54, 0.43 and 0.21. As for prediction method linear trend, Alpha were 0.999, 1.000 and 0.298. The average relative error between predicted value and actual value was 9.62%, 21.90% and 7.52%. Conclusion Winters multiplication model has practical value to predict school absence due to illness and provide scientific basis for early identification of abnormal signals.
- Exponential smoothing method /
- Time series /
- School absences due to illness /
- Prediction

HTML全文

图 1 2015年11月-2017年6月因病缺课人数

Figure 1. Number of absentees due to illness from November 2015 to June 2017

下载: 全尺寸图片幻灯片

图 2 简单季节模型残差图

Figure 2. Residual map of simple seasonal model

下载: 全尺寸图片幻灯片

图 3 温特斯加法模型残差图

Figure 3. Residual Map of Winters additive model

下载: 全尺寸图片幻灯片

图 4 温特斯乘法模型残差图

Figure 4. Residual map of winters multiplication model

下载: 全尺寸图片幻灯片

图 5 三种模型对2017年7-12月因病缺课人数实际值与预测值比较

Figure 5. Comparison of the actual and predicted values of the number of absentees due to illness from July to December 2017 by three models

下载: 全尺寸图片幻灯片

图 6 温特斯乘法模型拟合与预测

Figure 6. Fitting and Prediction of Winters Multiplication Model

下载: 全尺寸图片幻灯片

表 1 指数平滑法三种模型的拟合结果分析表

Table 1. Analysis table of fitting result of three models by exponential smoothing method

模型类型	R_adj²	R²	RMSE	正态化的BIC	Ljung-Box Q
模型类型	R_adj²	R²	RMSE	正态化的BIC	统计量	P值
简单季节模型	0.72	0.92	445.11	12.50	14.80	0.540
温特斯加法模型	0.72	0.93	420.99	12.54	15.32	0.430
温特斯乘法模型	0.77	0.98	258.75	11.56	19.16	0.210

下载: 导出CSV

表 2 各模型统计量分析

Table 2. Statistical analysis of three models

模型类型	指标	预测值	SE	t值	P值
简单季节模型	Alpha(水平)	0.999	0.241	4.148	0.001
	Delta(季节)	1.000	274.782	0.004	0.997
温特斯加法模型	Alpha(水平)	1.000	0.257	3.884	0.001
	Gamma(趋势)	0.001	0.055	0.015	0.988
	Delta(季节)	0.001	10 352.636	< 0.001	1.000
温特斯乘法模型	Alpha(水平)	0.298	0.045	6.631	< 0.001
	Gamma(趋势)	0.265	0.078	3.399	0.003
	Delta(季节)	0.999	0.149	6.712	< 0.001

下载: 导出CSV

表 3 三个模型对2017年7-12月因病缺课人数预测效果验证

Table 3. Validation of three models for predicting the number of absentees due to illness from July to December 2017

时间	实际值(人)	简单季节模型		温特斯加法模型		温特斯乘法模型
时间	实际值(人)	预测值(95% CI)	相对误差(%)	预测值(95% CI)	相对误差(%)	预测值(95% CI)	相对误差(%)
2017年7月	685	1 113(178~2 048)	38.45	1 419(531~2 307)	51.73	921(375~1 467)	25.62
2017年8月	27	178(-1 144~1 500)	84.83	485(-771~1 742)	94.43	53(-493~599)	49.06
2017年9月	3 991	2 989(1 370~4 608)	-33.52	3 298(1 758~4 837)	-21.01	2 498(-7 295~12 290)	-59.77
2017年10月	2 931	3 640(1 771~5 509)	19.48	3 951(2 172~5 729)	25.82	2 932(-11 121~16 986)	0.03
2017年11月	5 441	3 875(1 786~5 965)	-40.41	4 490(2 501~6 480)	-21.18	3 849(-18 030~25 728)	-41.36
2017年12月	5 327	4 795(2 506~7 084)	-11.10	5 413(3 232~7 593)	1.59	4 489(-25 131~34 109)	-18.67

下载: 导出CSV

表 4 温特斯乘法模型预测2018年1-3月因病缺课人数

Table 4. Winters multiplication model predicts the number of absentees due to illness from January to March 2018

时间	预测值	UCL^a	LCL^b
2018年1月	955	8 166	-6 257
2018年2月	22	598	-555
2018年3月	2 896	41 835	-36 044
注：^a预测值95%可信区间的上限；^b预测值95%可信区间的下限。

下载: 导出CSV

参考文献(19)

[1]	韩俊锋, 王子军. 我国2006-2008年学校传染病突发公共卫生事件分析[J]. 中国学校卫生, 2010, 31(4): 463-465. DOI: 10.16835/j.cnki.1000-9817.2010.04.036. Han JF, Wang ZJ. Analysis of the infectious events in school during 2006-2008 in China. [J]. Chin J Sch Health, 2010, 31(4): 463-465. DOI: 10.16835/j.cnki.1000-9817.2010.04.036.
[2]	尹浩, 赵琦, 周昌明, 等. 江西农村地区传染病症状监测数据报告质量及其影响因素研究[J]. 中华疾病控制杂志, 2016, 20(11): 1139-1143. DOI: 10.16462/j.cnki.zhjbkz.2016.11.016. Yin H, Zhao Q, Zhou CM, et al. Evaluation of data quality and influencing factors of integrated syndromic surveillance in rural Jiangxi Province, China[J]. Chin J Dis Control Prev, 2016, 20(11): 1139-1143. DOI: 10.16462/j.cnki.zhjbkz.2016.11.016.
[3]	苗开超. 基于指数平滑模型的农产品价格预测研究[D]. 合肥: 合肥工业大学, 2009. DOI: 10.7666/d.y1508013. Miao KC. Prediction of agricultural product price based on exponential smoothing[D]. Hefei: Hefei University of Technology, 2009. DOI: 10.7666/d.y1508013.
[4]	陈金先. 多种时间序列预测模型在市场营销预测中的比较[J]. 统计与决策, 2012, (12): 79-81. DOI: 10.13546/j.cnki.tjyjc.2012.12.014. Chen JX. Comparison of multiple time series forecasting models in marketing forecasting[J]. Statistics and Decision, 2012, (12): 79-81. DOI: 10.13546/j.cnki.tjyjc.2012.12.014.
[5]	翟志光. 传染病预测预警方法及应用进展(二)[J]. 中国中医药现代远程教育, 2012, 10(18): 161-163. DOI: 10.3969/j.issn.1672-2779.2012.16.115. Zhai ZG. Advances in methods and applications of infectious disease prediction and early warning(2)[J]. Chinese Medicine Modern Distance Education of China, 2012, 10(18): 161-163. DOI: 10.3969/j.issn.1672-2779.2012.16.115.
[6]	王山. 时间分布模型在甲肝流行趋势分析中的应用[D]. 杭州: 浙江大学, 2016. Wang S. Application of temporal distribution models on the incidence trend analysis of hepatitis A[D]. Hangzhou: Zhejiang University, 2016.
[7]	张翼飞. 三种呼吸道传染病发病情况时间序列预测研究[D]. 重庆: 第三军医大学, 2008. DOI: 10.7666/d.y1401934. Zhang YF. Research of time series predictive model on incidence of three kinds of respiratory infectious disease[D]. Chongqing: Third Military Medical University, 2008. DOI: 10.7666/d.y1401934.
[8]	马翠荣, 杨婕, 余小金. 江苏省2006-2014年城乡未成年人跌倒病例的时间序列预测分析[J]. 中华疾病控制杂志, 2018, 22(2): 122-125. DOI: 16462/j.cnki.zhjbkz.2018.02.005. Ma CR, Yang J, Yu XJ. The fall injury cases of urban and rural areas for minors in Jiangsu Province: a time-series prediction and analysis, 2006-2014[J]. Chin J Dis Control Prev, 2018, 22(2): 122-125. DOI: 16462/j.cnki.zhjbkz.2018.02.005.
[9]	唐金芳, 曾小云. 2005-2014年南宁市麻疹发病率ARIMA模型及其趋势预测[J]. 中华疾病控制杂志, 2016, 20(7): 738-740. DOI: 10.16462/j.cnki.zhjbkz.2016.07.023. Tang JF, Zeng XY. ARIMA model of measles incidence and its trend prediction from 2005 to 2014 in Nanning City[J]. Chin J Dis Control Prev, 2016, 20(7): 738-740. DOI: 10.16462/j.cnki.zhjbkz.2016.07.023.
[10]	张磊, 刘艳红. 季节性指数平滑法预测深圳市宝安区涂阳肺结核发病人数的应用[J]. 中国医药导报, 2015(18): 39-42. https://www.cnki.com.cn/Article/CJFDTOTAL-YYCY201518012.htm Zhang L, Liu YH. Prediction of the onset number of smear positive pulmonary tuberculosis in Baoo'an district of Shenzhen City with seasonal exponential smoothing method[J]. China Medical Herald, 2015(18): 39-42. https://www.cnki.com.cn/Article/CJFDTOTAL-YYCY201518012.htm
[11]	Rimaityte I, Ruzgas T, Denafas G, et al. Application and evaluation of forecasting methods for municipal solid waste generation in an eastern-European city[J]. Waste Manag Res, 2012, 30(1): 89-98. DOI: 10.1177/0734242X10396754.
[12]	吴健华, 李培月, 钱会. 基于Holt指数平滑模型的地下水水质预测[J]. 工程勘察, 2013, 41(10): 38-41. DOI: 10.3969/j.issn.1000-1433.2013.10.008.Wu JH, Li PY, Qian H. Groundwater quality prediction based on holt exponential smoothing model[J]. Geotechnical Investigation & Surveying, 2013, 41(10): 38-41. DOI: 10.3969/j.issn.1000-1433.2013.10.008.
[13]	傅伟杰, 谢昀, 曾志笠, 等. 三种模型在江西省流感样病例预测中的应用与比较[J]. 中华疾病控制杂志, 2019, 23(1): 101-105. DOI: 10.16462/j.cnki.zhjbkz.2019.01.021. Fu WJ, Xie Y, Zeng ZL, et al. Application and comparison of three models for the prediction of influenza-like illness in Jiangxi Province[J]. Chin J Dis Control Prev, 2019, 23(1): 101-105. doi: 10.16462/j.cnki.zhjbkz.2019.01.021
[14]	周炳飞. 动态指数平滑模型预测及应用[J]. 哈尔滨师范大学自然科学学报, 2013, 29(4): 25-27. DOI: 10.3969/j.issn.1000-5617.2013.04.008. Zhou BF. Forecasting of dynamic exponential smoothing model and its application[J]. Natural Science Journal of Harbin Normal University, 2013, 29(4): 25-27. DOI: 10.3969/j.issn.1000-5617.2013.04.008.
[15]	王玉明, 孟蕾, 李娟生. 指数平滑法在黑热病发病预测中的应用[J]. 地方病通报, 2010, 25(3): 24-25. DOI: 10.13215/j.cnki.jbyfkztb.2010.03.035. Wang YM, Meng L, Li JS. Application of exponential smoothing in prediction of Kala-azar incidence[J]. Endemic Diseases Bulletin, 2010, 25(3): 24-25. DOI: 10.13215/j.cnki.jbyfkztb.2010.03.035.
[16]	朱奕奕, 赵琦, 冯玮, 等. 应用指数平滑法预测上海市甲型病毒性肝炎发病趋势[J]. 中国卫生统计, 2013, 30(1): 31-33. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGWT201301010.htm Zhu YY, Zhao Q, Feng W, et al. The application of exponential smoothing methods on the forecast of hepatitis A in Shanghai[J]. Chinese Journal of Health Statistics, 2013, 30(1): 31-33. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGWT201301010.htm
[17]	González Díaz A, Sánchez Valdés L, Armas Pérez L, et al. Trends and predictions of tuberculosis, and challenges towards tuberculosis eradication in Havana City[J]. Rev Cubana Med Trop, 2012, 64(2): 163-175. http://www.ncbi.nlm.nih.gov/pubmed/23444635
[18]	孙乔, 袁政安, 陶芳芳, 等. 温特斯乘法模型在呼吸道症候群监测中的应用[J]. 中华疾病控制杂志, 2011, 15(10): 905-908. http://zhjbkz.ahmu.edu.cn/article/id/JBKZ201110025 Sun Q, Yuan ZA, Tao FF, et al. Application of the prediction model of winters method-multiplicative in respiratory syndrome surveillance[J]. Chin J Dis Control Prev, 2011, 15(10): 905-908. http://zhjbkz.ahmu.edu.cn/article/id/JBKZ201110025
[19]	唐广心, 张飞飞, 鲁苇葭, 等. 指数平滑法在麻疹发病率预测中的应用[J]. 实用预防医学, 2018, 25(6): 757-759. DOI: 10.3969/j.issn.1006-3110.2018.06.034. Tang GX, Zhang FF, Lu WJ, et al. Application of exponential smoothing method to forecasting the incidence rate of measles[J]. Practical Preventive Medicine, 2018, 25(6): 757-759. DOI: 10.3969/j.issn.1006-3110.2018.06.034.