Current risk status and spatial distribution of COVID-19 in China based on the day-on-day growth rate and spatial constrained clustering algorithm
-
摘要:
目的 分析中国31个省、自治区、直辖市和新疆生产建设兵团(以下简称“31个省(区、市、兵团)”)新型冠状病毒肺炎(coronavirus disease 2019, COVID-19)疫情的近期防控态势, 基于各省份的疫情防控现状提出分区管理的设计建议。 方法 基于2020年1月25—2月8日中国31个省(区、市、兵团)COVID-19累计确诊病例数, 计算累计和新增确诊病例数的环比增长率, 并拟合随时间的线性函数得到环比增长率的线性趋势。进一步结合环比增长率的中位数(median, M)、标准差(standarddeviation, S)和累计确诊病例数进行AZP-SA(auto zone procedure with stimulate annealing, AZP-SA)的空间约束聚类, 对各省份疫情现状进行合理分区。 结果 中国31个省(区、市、兵团)累计确诊病例数的环比增长率在近期均呈现下降趋势。新增确诊病例数的环比增长率则没有呈现出明显的趋势方向。选择AZP-SA方法将中国31个省(区、市、兵团)分成8个区, 其中湖北及湖北周边省份属于疫情下降相对较慢的地区, 西北和北方省份疫情控制良好, 东部和东南省份的疫情控制效果处于两者之间。 结论 累计确诊病例数的环比增长率是衡量疫情短期趋势的良好指标, 基于累计确诊病例数及其环比增长率应用空间约束聚类可以对中国各省份的疫情现状进行划分, 为下一步的复工复产提供建议。 Abstract:Objective Analyze the current situation of COVID-19 epidemic prevention and control in various provinces in China, and propose a regionalized management method based on current status of epidemic prevention and control. Methods We calculated day-of-day growth rate of cumulative and new confirmed cases based on the reported confirmed cases between Jan 25 to Feb 8, and fitted it with the linear regression model accompanied with date. Furthermore, we applied auto zone procedure with simulator annealing(AZP-SA) spatial constrained clustering in cumulative confirmed cases and the linear trend, median, standard deviation of the growth rate, and provided a regionalized management suggestion based on previous result. Results The growth rate of cumulative confirmed cases in all provinces has shown a downward trend in recent. The growth rate of new confirmed cases did not show a significant trend. AZP-SA method partitions the mainland China into 8 regions. Region surrounding Hubei with relatively slow decline trend, and regions of the northwest and north provinces have good control of epidemic situation, and the eastern and Southeast provinces have a control effect between them. Conclusions The growth rate of the cumulative confirmed cases is a good indicator to measure the short-term trend of the epidemic. Based on the cumulative confirmed cases and its growth rate, the application of spatial constraint clustering can partitions the epidemic status of China, and provide a regionalized management for work resumption. -
2019年12月起, 在武汉市发现一种严重急性呼吸综合征冠状病毒2(severe acute respiratory syndrome coronavirus 2, SARS-CoV-2)引起的新型冠状病毒肺炎(coronavirus disease 2019, COVID-19)疫情[1-2]。相较于其他两种冠状病毒, 严重急性呼吸系统综合征冠状病毒(severe acute respiratory syndrome-coronavirus, SARS-CoV)和中东呼吸综合征冠状病毒(middle east respiratory syndrome-coronavirus, MERS-CoV), SARS-CoV-2的死亡率较低但传染性远超过前者, 不仅给人民的生命财产带来重大威胁, 也给国家带来了巨大损失。根据国家卫生健康委员会公告, 截至2020年2月23日, 全国累计确诊病例77 150例, 死亡2 592例[3]。
尽管此次COVID-19疫情波及全国, 但各个省份的严重程度却有很大差异, 而且不同省份和地区的经济实力与医疗资源存在一定的差异, 因此不同地区防控措施的实施情况与效果可能存在一定差异。空间约束聚类是一种常用的指导分区管理的理论方法。空间约束聚类即在满足聚类的空间实体邻接约束的基础上寻找聚类内属性数据同质性程度最高的聚类方案。由于得到的聚类结果既满足属性数据同质性程度较高, 又符合聚类在空间上的邻接和紧凑, 因此常常用于分区管理中[4-5]。
本研究采取科学的方法针对不同地区的疫情现状进行分区统计, 提出分区复工复产的设计建议。因此, 本研究提出基于环比增长率的方法, 分析中国COVID-19的疫情发展状况, 对不同省份的新增和累计确诊病例数的环比增长率的变化情况进行比较, 从而对各省份的疫情防控效果情况作出初步评价。继而结合各省份累计确诊病例数、环比变化率的中位数(median, M)、标准差(standarddeviation, S)和线性趋势系数进行空间约束聚类, 从空间角度进行风险区域划分, 以期为疫情的重点防控提供科学的依据。
1. 对象与方法
1.1 数据来源
研究的数据来源于中国国家卫生健康委员会及31个省(区、市、兵团)卫生健康委员会网站每日公布的COVID-19疫情通报, 以每日每个省份的累计和新增确诊病例数为核心数据, 包括了中国31个省、自治区、直辖市和新疆建设兵团。其中, 新疆自治区和新疆建设兵团的确诊病例数都记作新疆地区的确诊病例数。由于2020年1月20日之前仅有武汉市卫生健康委员会进行了疫情通报, 且1月20日之后的几日, 各地的确诊病例报告规范可能不统一, 确诊标准存在差异, 报告质量可能较低, 为了避免在统计结果中引入噪音, 本研究选择的研究时间范围为2020年1月25日―2月8日。截至2月8日西藏仅有1例来自湖北省的输入型确诊病例, 因此西藏不纳入本次统计分析。
1.2 统计学方法
为描述中国31个省(区、市、兵团)的COVID-19疫情进展情况, 本研究首先计算了各省份每日累计确诊病例数和新增确诊病例数的环比增长率(rt): $r_{t}=\frac{C_{t}}{C_{t-1}}-1$
然后基于各省份的环比增长率用线性回归模型拟合增长率的趋势(r):r=β0+β1T+ε
基于环比增长率线性回归模型的系数β1初步判断各省疫情的短期趋势。β1为负, 提示当地的防控效果在逐渐好转, β1为正, 说明当地的防控效果持续在变差, 从而评价各地的防控效果。
最后, 基于累计确诊病例数的环比增长率的中位数、标准差、线性趋势系数β1、以及累计确诊病例进行空间约束聚类, 由于前三者都是衡量疫情的变化趋势, 即反映了疫情防控的效果, 而累计确诊病例数衡量了现存的疫情严重程度, 如果在计算各地区疫情风险相似性时给定相同权重, 则疫情变化趋势的影响会大于现存疫情风险。本研究不对疫情防控中现存和变化趋势的重要性做假设, 因此我们将权重设置为1/6、1/6、1/6和1/2, 这样在计算不同地区的疫情风险相似性时, 疫情现存和变化趋势的重要性就一致了。聚类方法选择AZP-SA(auto zone procedure with stimulate annealing)[6-7], AZP是空间约束聚类方法的一种实现, 这是一种基于启发式算法进行组合优化的空间约束聚类方法。原理简述如下:即先初始化一个随机的满足空间邻接的聚类方案, 然后基于最大化聚类内属性数据同质性的目标, 采用启发式算法迭代地优化聚类方案, 得到最终的“最优”空间约束聚类结果。因为空间约束聚类问题是一个NP完全问题, 所以只能得到近似最优的结果。AZP步骤中的启发式算法有多种常见的选择, 本研究选择的是模拟退火法(stimulate annealing), 因为这种方法速度快、实现简单且效果也相对较好, 应用很广[8]。由于AZP在迭代优化中有很多随机的步骤, 因此每次运行的结果存在一定差异, 为了减少偶然因素的影响, 本研究重复运行了500次AZP-SA算法, 选择其中同质性程度最高的方案。AZP-SA方法需要预先给定聚类数, 由于没有任何先验的合理的聚类数参考, 本研究在预实验过程中对2~12聚类数都进行了空间约束聚类, 采用内部聚类验证指标Calinski-Harabasz指数来指示最佳的聚类数[9]。Calinski-Harabasz指标是描述聚类的类间离散型与类内离散型之比:
$$ Calinski \;Harabasz=\frac{tr\left(B_{k}\right)}{tr\left(W_{k}\right)} \times \frac{n_{E}-k}{k-1}$$ (1) 其中, tr(Bk)是类间离散矩阵的迹, tr(Wk)是类内离散矩阵的迹, nE是数据的规模, k是聚类数。因此Calinski-Harabasz指标越大, 则说明聚类效果越好, 且乘号右侧的项防止指标偏好k更大的结果。因此, Calinski-Harabasz指标能够用于比较不同聚类数结果的优劣。
最后对聚类结果进行描述和疫情风险特征说明。海南省由于地理环境与其他省份存在明显差异, 因此空间约束聚类没有加入海南省。统计分析使用R3.5.3软件, 数据可视化使用ARCGIS 10.4.1软件。检验水准α=0.05。
2. 结果
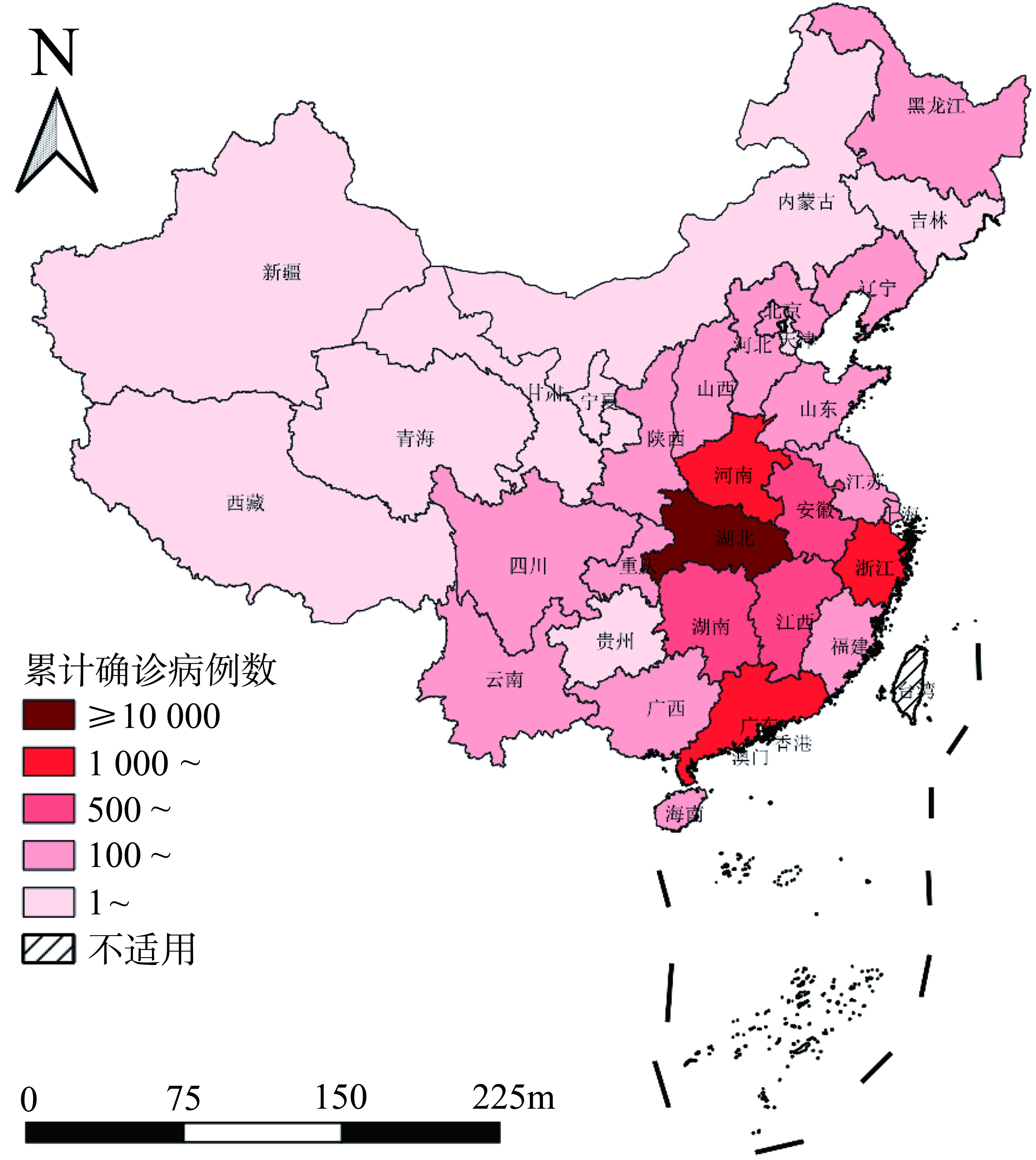
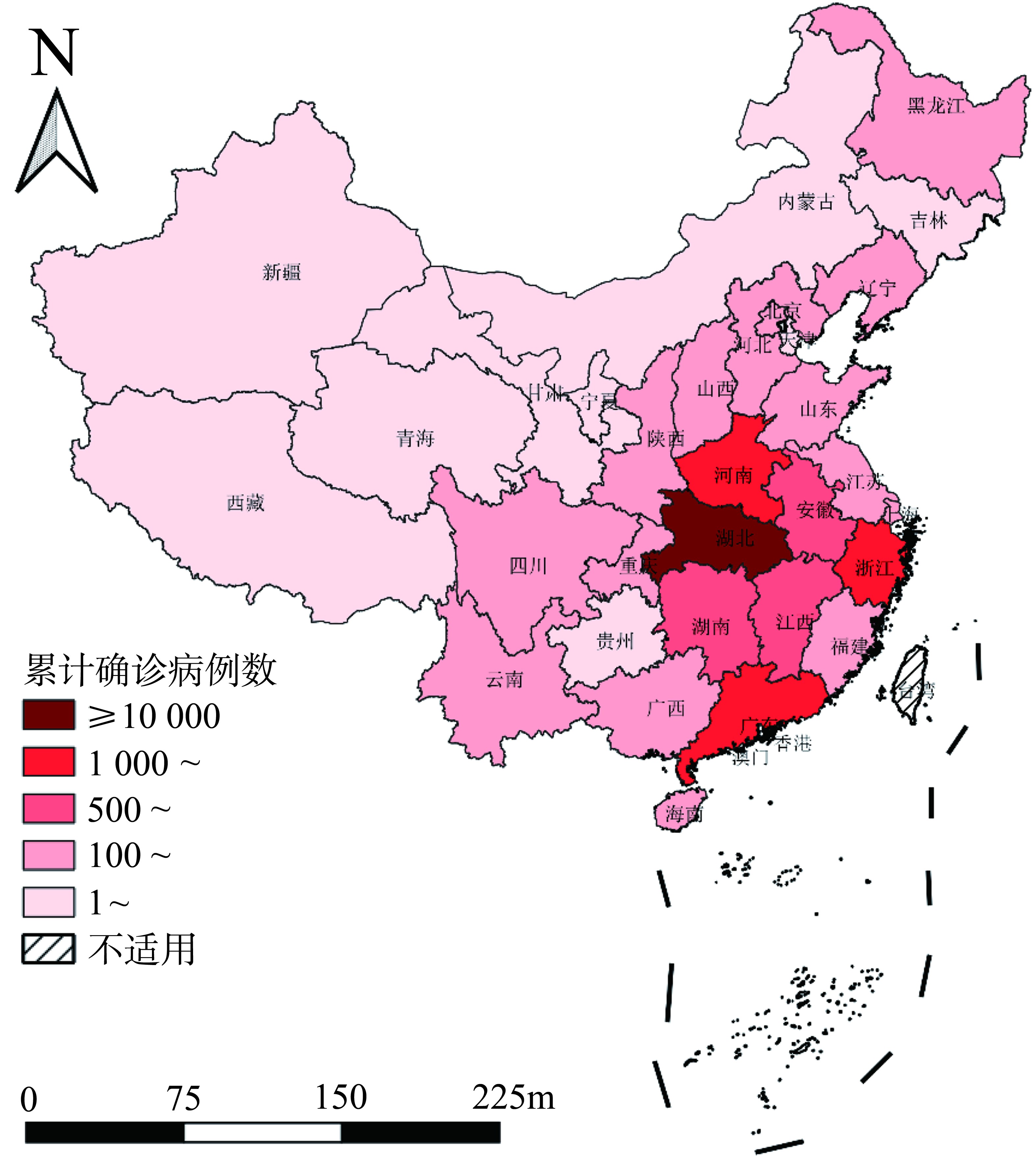
中国31个省(区、市、兵团)2020年2月8日的COVID-19累计确诊病例数见图 1, COVID-19疫情分布呈现明显的空间分布差异, 绝大多数确诊病例集中在湖北省, 与湖北省交界的河南、湖南、安徽等省份疫情也相对严重, 而西北和西南地区的疫情相对较低。浙江省和广东省的累计确诊人数比湖北周边省份更严重。
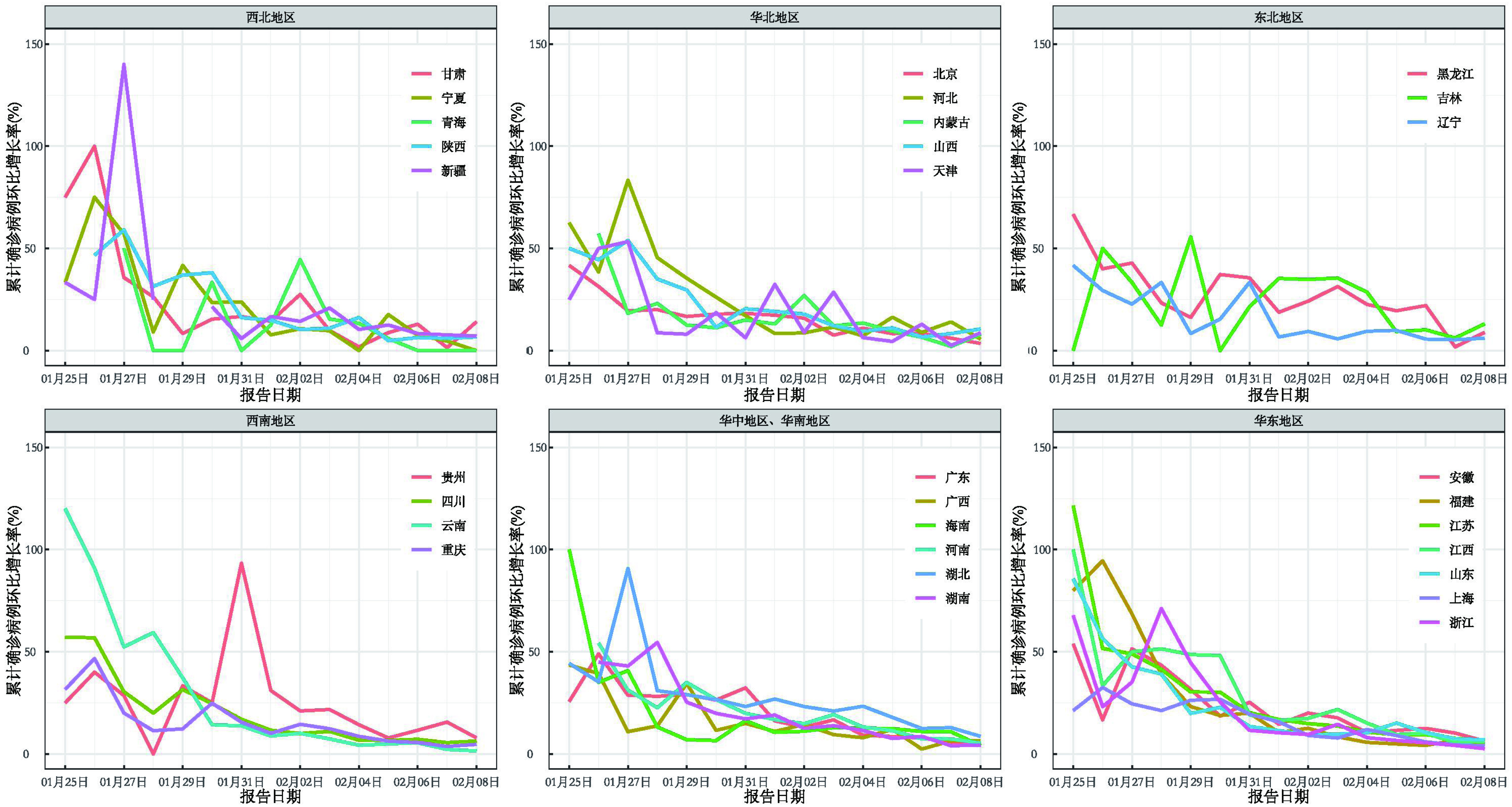
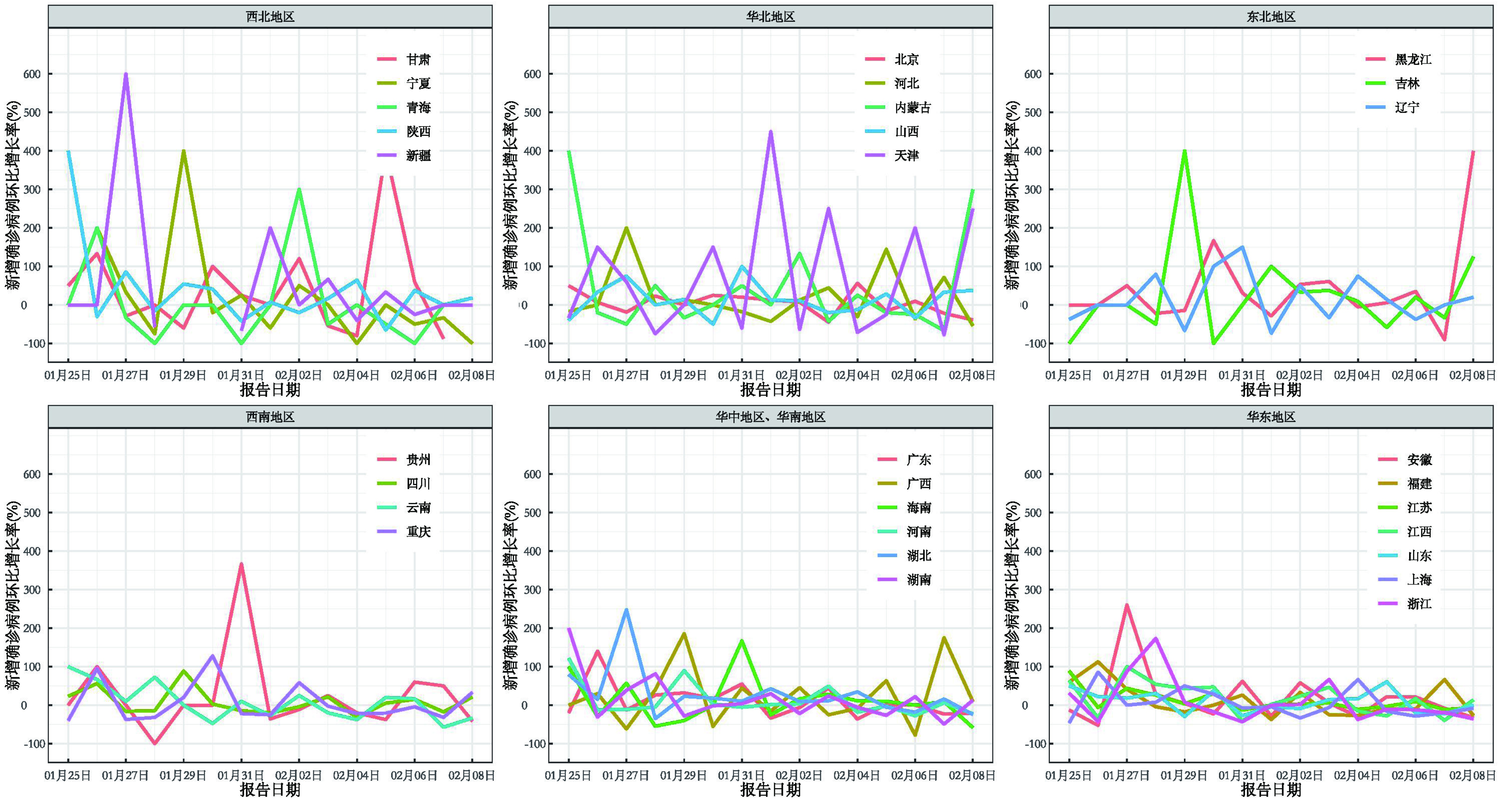
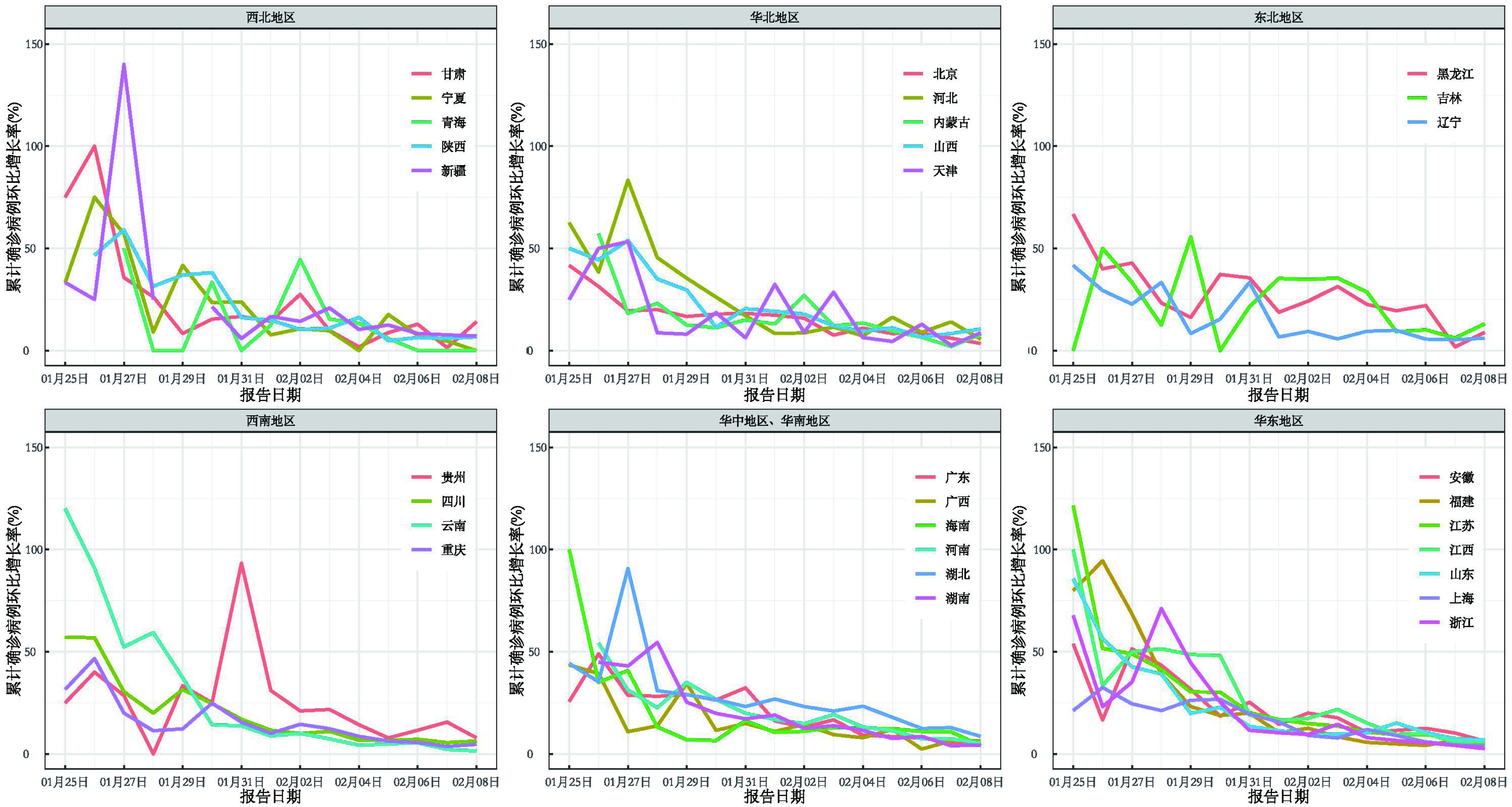
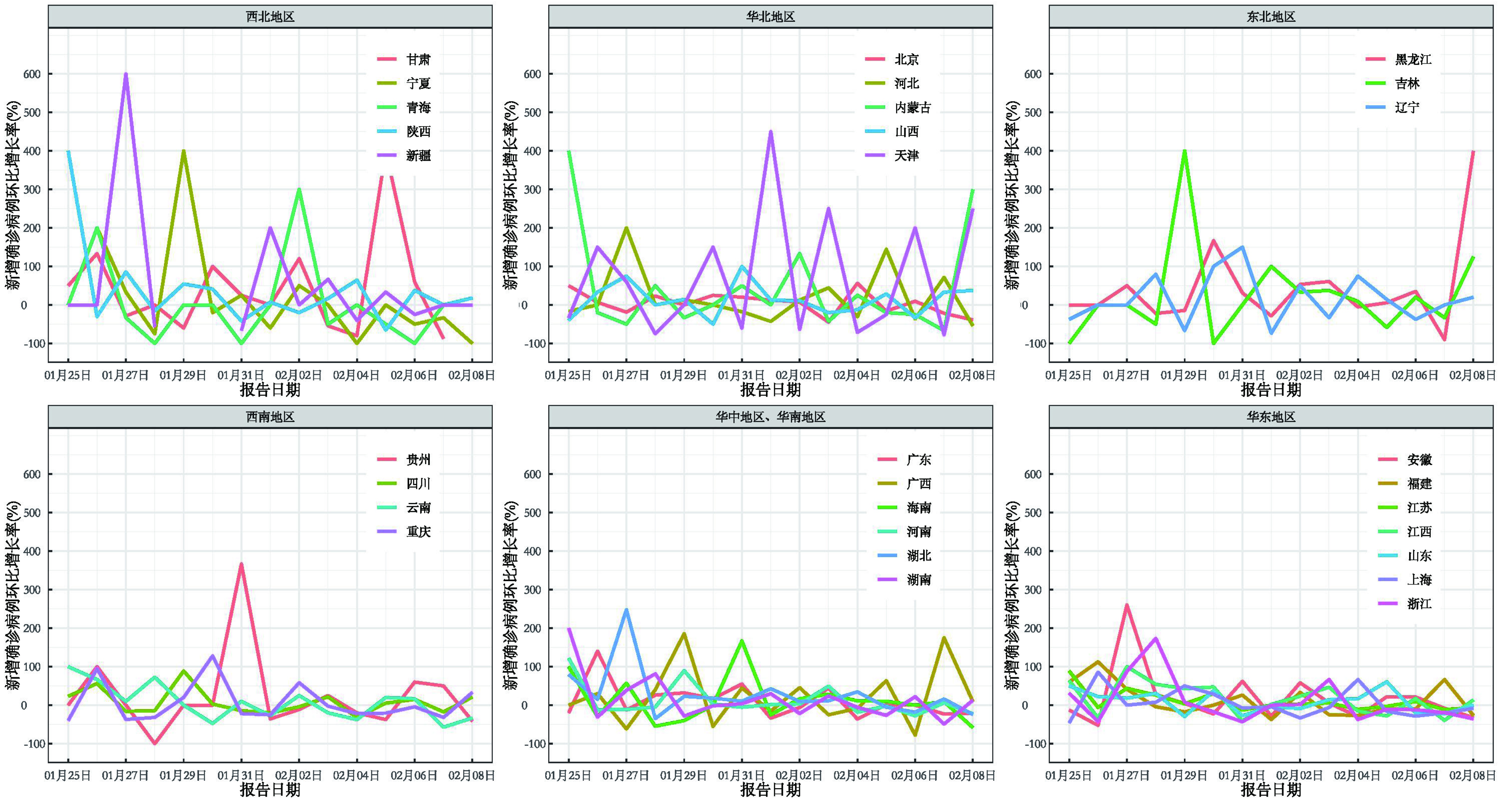
图 1 我国2020年2月8日各省市的COVID-19累计确诊病例数分布图Figure 1. Distribution of COVID-19 cumulative confirmed cases by provinces and cities in China in February 8, 2020从累计确诊病例数的环比增长率的时间序列图看, 几乎所有省份的COVID-19疫情的累计确诊病例数增长在近期均开始出现平稳下降趋势, 尤其是华东地区和华中地区等疫情高发地区, 环比增长率的下降趋势非常明显。新增确诊病例数的环比增长率从图中没有表现出任何明显趋势, 近20余日都在0%附近震荡, 见图 2、图 3。
图 2 中国COVID-19累计确诊病例数的环比增长率曲线Figure 2. Dod growth curve of COVID-19 cumulative confirmed cases in provinces and cities in mainland China
图 3 中国COVID-19新增确诊病例数的环比增长率曲线Figure 3. Dod growth rate of COVID-19 newly confirmed cases in provinces and cities in mainland China基于各省份的COVID-19累计确诊病例数的环比增长率拟合的线性回归模型结果见表 1。所有省份的累计确诊病例数的环比增长率的线性趋势系数为负。从线性趋势来看, 其中吉林、贵州、新疆、青海、内蒙古、天津、海南的环比增长率下降趋势并不明显。此外, 与湖北省毗邻的河南、湖南、陕西等地区, 疫情增长趋势的缓和趋势相较华东地区较慢。
表 1 中国COVID-19累计确诊病例数的环比增长率的线性模型系数Table 1. Linear model coefficients of the dod growth rate of COVID-19 cumulative confirmed cases in mainland China省份 β1值 t值 P值 R2(%) 省份 β1值 t值 P值 R2(%) 吉林 -0.011 -1.017 0.328 7.37 辽宁 -0.022 -4.561 0.001 61.54 贵州 -0.016 -1.280 0.223 11.19 浙江 -0.040 -4.643 < 0.001 62.38 新疆 -0.033 -1.776 0.099 19.52 重庆 -0.021 -4.656 < 0.001 62.52 青海 -0.097 -2.103 0.057 26.94 安徽 -0.027 -4.789 < 0.001 63.82 内蒙古 -0.076 -2.368 0.034 30.13 河北 -0.041 -4.817 < 0.001 64.10 天津 -0.021 -2.627 0.021 34.67 江苏 -0.053 -4.848 < 0.001 64.38 海南 -0.034 -2.867 0.013 38.74 山东 -0.041 -5.170 < 0.001 67.28 河南 -0.057 -3.298 0.006 45.55 江西 -0.048 -5.575 < 0.001 70.51 湖南 -0.069 -3.330 0.005 46.03 云南 -0.069 -5.747 < 0.001 71.76 陕西 -0.075 -3.354 0.005 46.40 福建 -0.057 -5.803 < 0.001 72.15 湖北 -0.031 -3.544 0.004 49.14 四川 -0.034 -6.394 < 0.001 75.88 甘肃 -0.044 -3.610 0.003 50.06 广东 -0.025 -6.620 < 0.001 77.12 广西 -0.021 -4.081 0.001 56.16 山西 -0.032 -6.814 < 0.001 78.13 宁夏 -0.037 -4.156 0.001 57.05 北京 -0.020 -7.255 < 0.001 80.19 黑龙江 -0.027 -4.346 0.001 59.23 上海 -0.019 -7.594 < 0.001 81.60 基于31个省(区、市、兵团)的COVID-19新增确诊病例数的环比增长率拟合的线性模型系数结果显示, 大多数省份的线性趋势系数为负。所有省份的线性趋势都不明显。截至目前本次疫情在中国北方省份相对较轻, 但是甘肃、黑龙江、天津、吉林、辽宁、山西等北方省份的新增确诊病例数的环比增长率趋势仍为正, 见表 2。
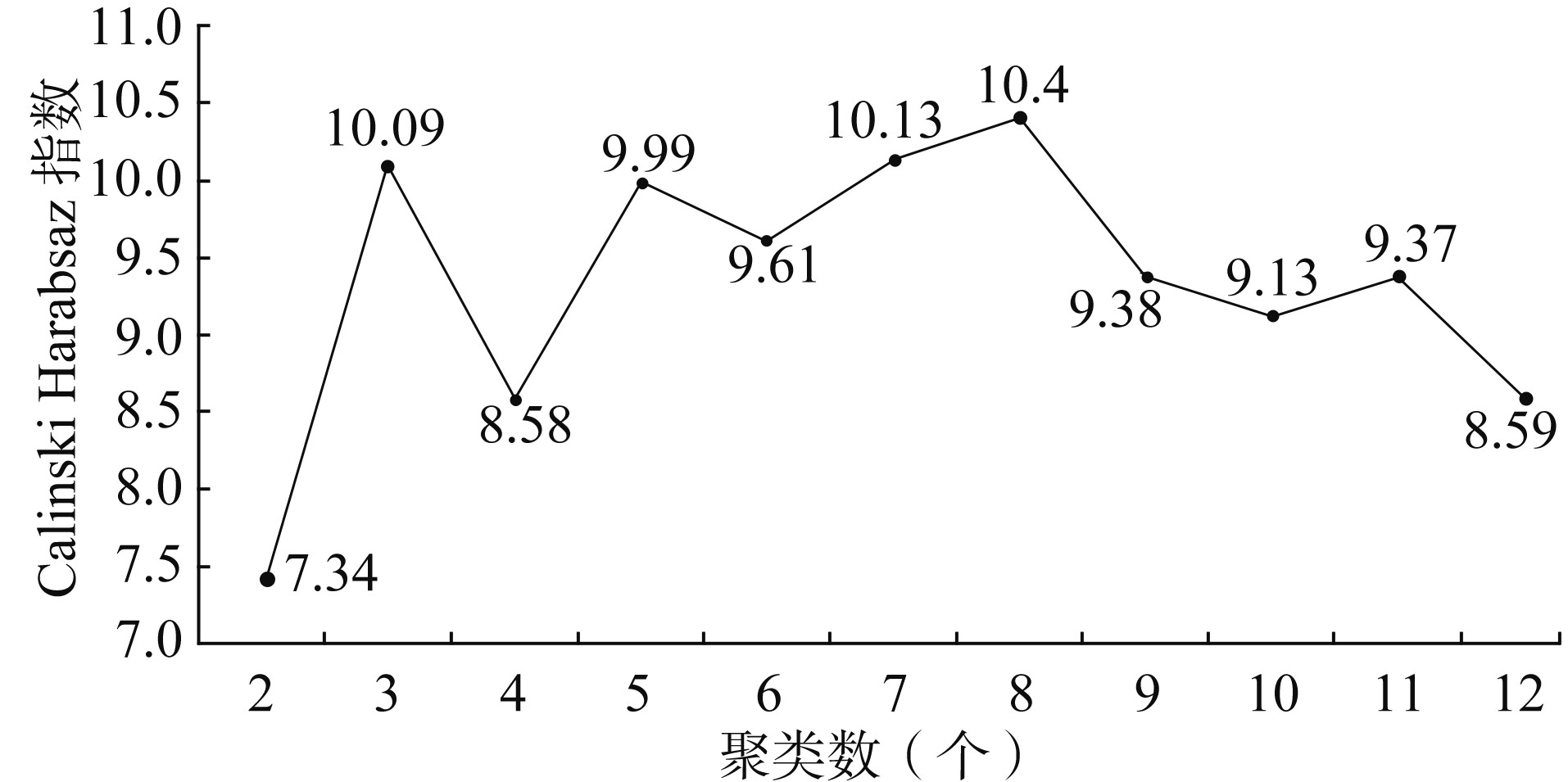
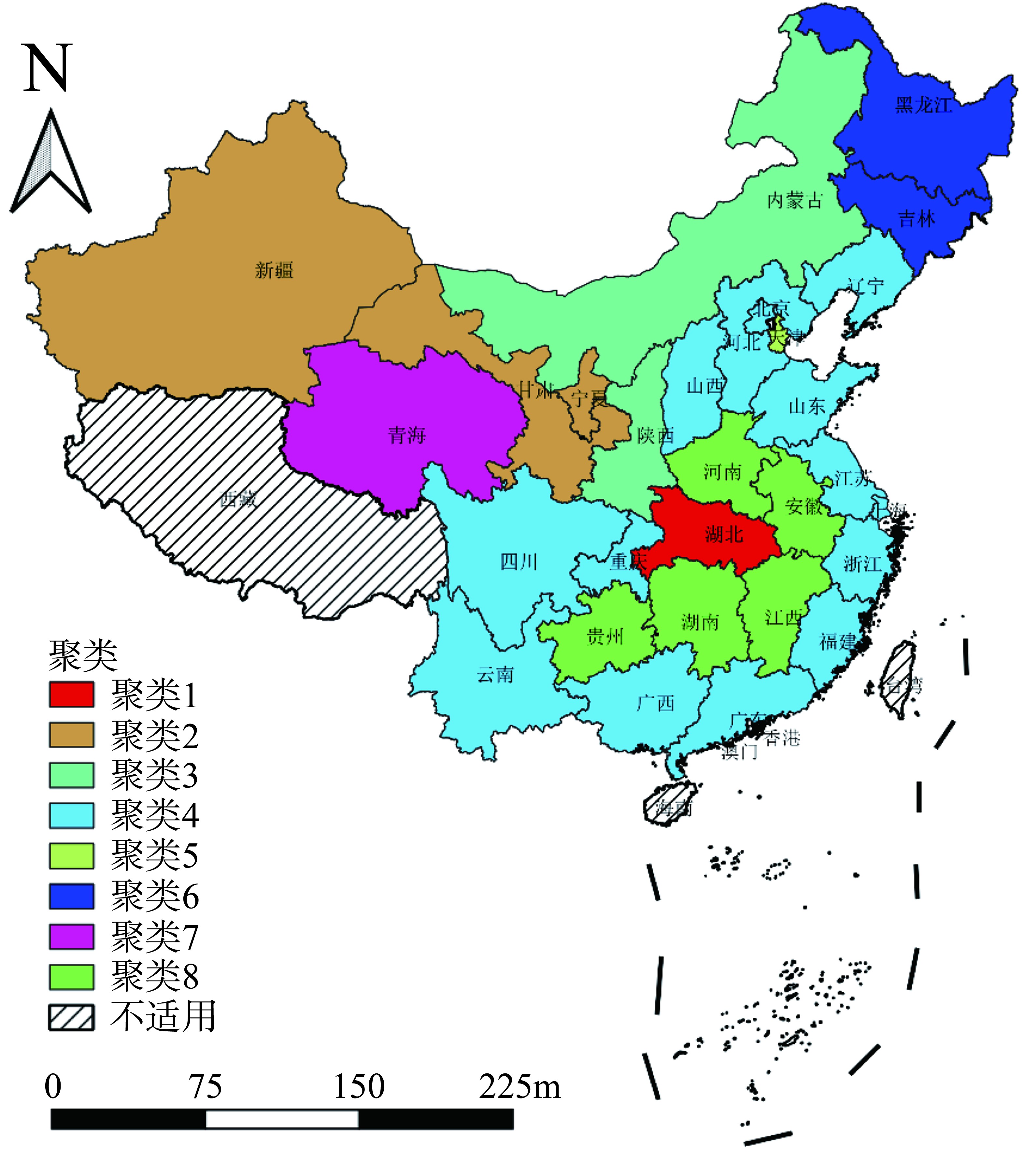
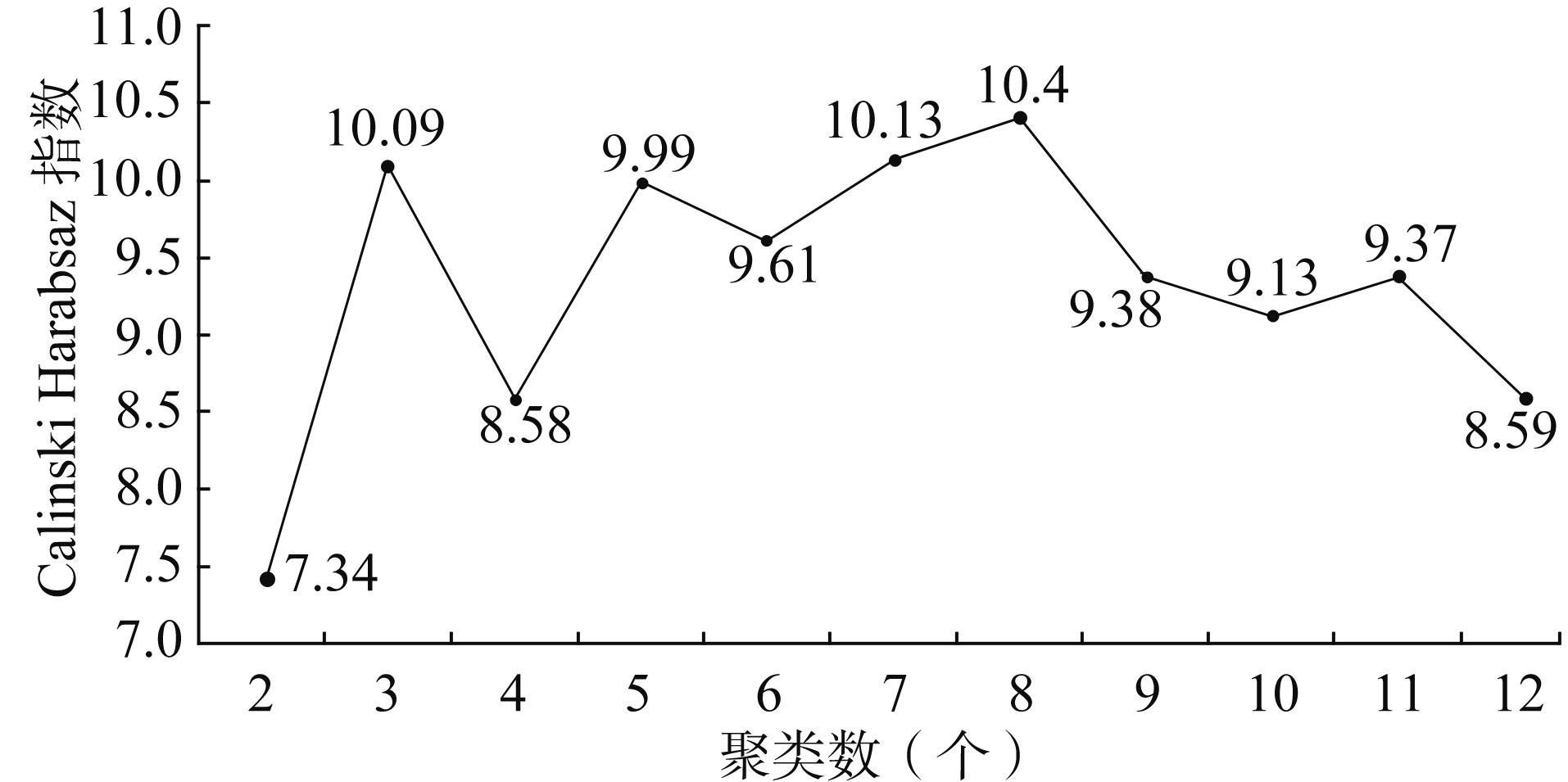
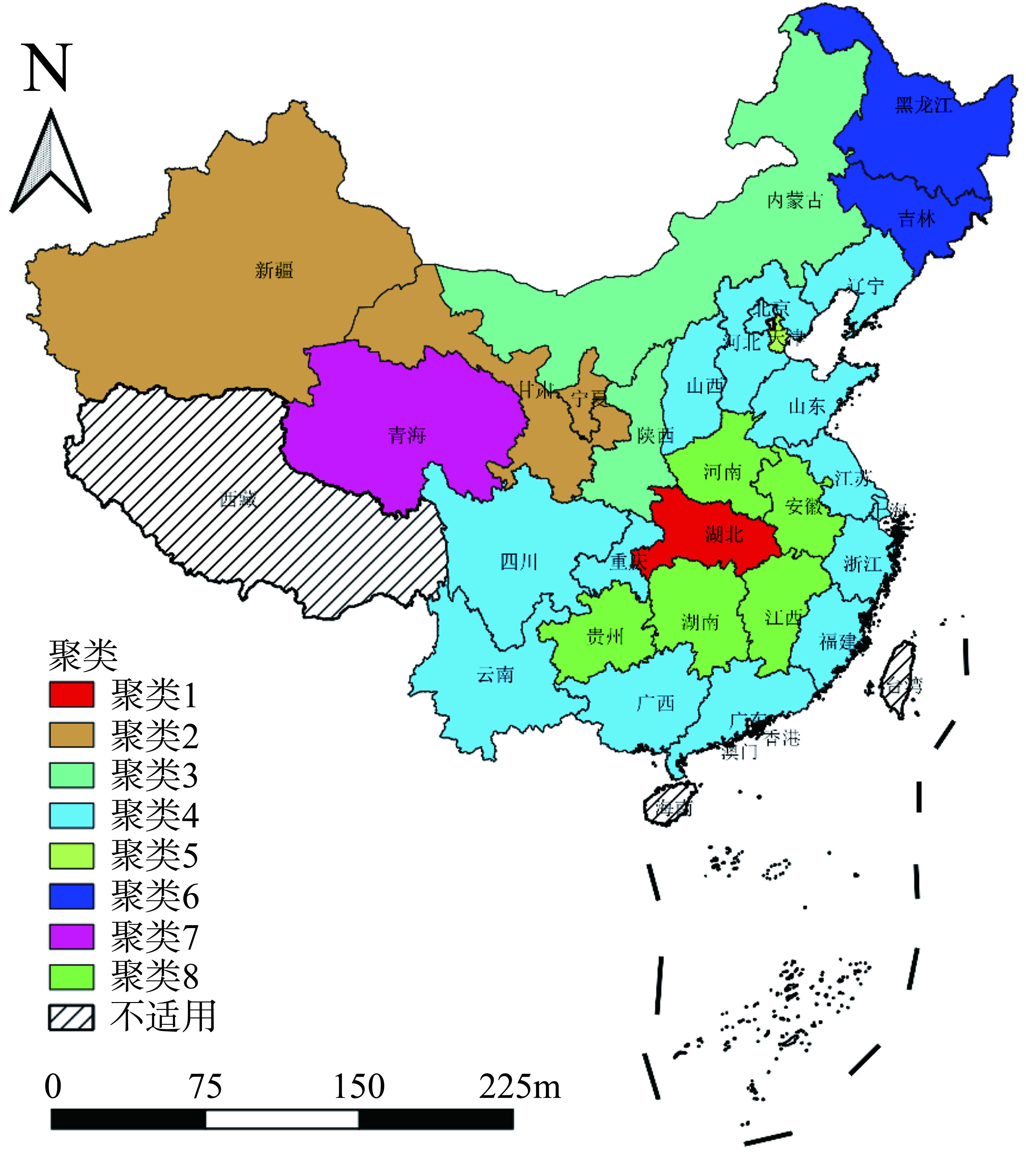
表 2 中国COVID-19新增确诊病例数的环比增长率的线性模型系数Table 2. Linear model coefficients of the dod growth rate of COVID-19 newly confirmed casesin mainland China省份 β1 t值 P值 R2(%) 省份 β1 t值 P值 R2(%) 甘肃 0.228 1.592 0.135 16.32 四川 -0.019 -1.007 0.332 7.24 黑龙江 0.076 1.133 0.278 8.98 上海 -0.023 -1.042 0.316 7.71 天津 0.054 0.544 0.596 2.22 山东 -0.021 -1.246 0.235 10.67 广西 0.015 0.323 0.752 0.80 浙江 -0.053 -1.572 0.140 15.98 吉林 0.016 0.176 0.863 0.28 陕西 -0.105 -1.721 0.109 18.56 辽宁 0.000 0.009 0.993 0.00 广东 -0.044 -1.737 0.106 18.84 山西 0.000 0.008 0.994 0.00 北京 -0.028 -1.739 0.106 18.88 贵州 -0.019 -0.270 0.792 0.60 宁夏 -0.136 -1.782 0.100 20.93 河北 -0.016 -0.368 0.719 1.03 河南 -0.043 -1.809 0.094 20.11 重庆 -0.012 -0.387 0.705 1.14 福建 -0.044 -1.847 0.088 20.79 内蒙古 -0.034 -0.416 0.684 1.31 湖北 -0.068 -1.849 0.087 20.83 新疆 -0.053 -0.418 0.682 1.33 江西 -0.044 -1.899 0.080 21.71 青海 -0.077 -0.593 0.572 4.78 湖南 -0.066 -1.995 0.067 23.43 海南 -0.030 -0.836 0.418 5.10 江苏 -0.038 -2.894 0.013 39.18 安徽 -0.041 -0.909 0.380 5.97 云南 -0.068 -3.142 0.008 43.16 空间约束聚类预实验中, 聚类数从2~12的聚类结果的Calinski-Harabasz指数如图 4所示, 8聚类的Calinski-Harabasz指数最大, 即8聚类是相对较好的聚类数选择。(1)湖北单独为一类; (2)新疆、甘肃和宁夏为一类; (3)陕西和内蒙古为一类; (4)北京、福建、广东、广西、河北、江苏、辽宁、山东、山西、上海、四川、云南、浙江和重庆为一类; (5)天津为一类; (6)黑龙江和吉林为一类; (7)青海为一类; (8)安徽、贵州、河南、湖南和江西为一类。见图 5和表 3。
图 4 空间约束聚类中聚类数目与Calinski-Harabasz指数的关系图Figure 4. Relationship between the number of clusters and the Calinski-Harabasz index in spatially constrained clustering
图 5 中国COVID-19空间聚类分布地图Figure 5. Spatial clustering distribution map of COVID-19 in provinces and cities in mainland China表 3 中国COVID-19聚类结果Table 3. COVID-19 clustering results of provinces and cities in China聚类 省份 累计确诊病例数(个) 环比增长率 M值 S值 线性趋势系数 1 湖北省 27 100 0.23 0.20 -3.54 x值 27 100 0.23 0.20 -3.54 S2值 2 甘肃省 81 0.14 0.28 -3.61 宁夏回族自治区 45 0.11 0.22 -4.16 新疆维吾尔自治区 45 0.14 0.34 -1.78 x值 57 0.13 0.28 -3.18 S2值 17 0.02 0.05 1.02 3 内蒙古自治区 54 0.13 0.62 -2.37 陕西省 208 0.16 0.49 -3.35 x值 131 0.15 0.55 -2.86 S2值 77 0.02 0.06 0.49 4 北京市 326 0.17 0.10 -7.25 福建省 250 0.13 0.30 -5.80 广东省 1 120 0.17 0.13 -6.62 广西壮族自治区 195 0.12 0.13 -4.08 河北省 206 0.16 0.23 -4.82 江苏省 468 0.17 0.30 -4.85 辽宁省 105 0.09 0.12 -4.56 山东省 435 0.13 0.23 -5.17 山西省 115 0.18 0.16 -6.81 上海市 292 0.16 0.09 -7.59 四川省 386 0.12 0.17 -6.39 云南省 140 0.10 0.36 -5.75 浙江省 1 075 0.12 0.22 -4.64 重庆市 446 0.12 0.12 -4.66 x值 397 0.14 0.19 -5.64 S2值 309 0.03 0.08 1.08 5 天津市 88 0.09 0.16 -2.63 x值 88 0.09 0.16 -2.63 S2值 6 黑龙江省 307 0.23 0.16 -4.35 吉林省 78 0.21 0.17 -1.02 x值 193 0.22 0.17 -2.68 S2值 115 0.01 0.01 1.66 7 青海省 18 0.06 0.76 -1.64 x值 18 0.06 0.76 -1.64 S2值 8 安徽省 779 0.18 0.15 -4.79 贵州省 96 0.22 0.22 -1.28 河南省 1 033 0.19 0.38 -3.30 湖南省 838 0.17 0.46 -3.33 江西省 740 0.19 0.26 -5.58 x值 697 0.19 0.29 -3.65 S2值 317 0.02 0.11 1.47 3. 讨论
COVID-19疫情发展迅速, 是近年来最严重的传染病暴发事件。尽管中国现阶段仍有新增COVID-19疫情报道, 但全国范围内的防控措施已取得了阶段性成效[10], 从图 2可以看出, 几乎所有省份COVID-19的累计确诊病例数的环比增长率均呈下降趋势。所有省份的累计确诊病例数的环比增长率的线性趋势系数为负(表 1), 全国各省份COVID-19疫情进展均趋于平缓, 显示疫情已经由暴发期进入了平台期, 也进一步证实全国范围内疫情增长都已出现缓和迹象[11]。在线性回归分析模型中, 吉林、贵州、新疆等省份累计确诊病例环比增长率的下降趋势相对较低, 可能是由于累计确诊病例数非常少(< 100例)导致。湖北数据也没有得到高度的拟合, 与湖北存在较多病例, 每日的确诊病例与检测量有关, 真实病例的变化趋势可能难以根据报告数据表现。此外, 与湖北省毗邻的河南、湖南、陕西等省份, 疫情增长趋势缓比华东地区较慢, 可能是在全国性防控措施实施之前, 这些地区已经积累了大量潜在感染人群[12], 因此目前仍会有较大的确诊病例增长, 这些地区疫情防控任务艰巨, 未来一段时间仍需加强防控力度, 防止疫情反弹。
新增确诊病例数的环比增长率尚未有明显的趋势方向(图 3), 新增确诊病例的速度没有进一步加快, 说明全国疫情暂时从暴发阶段进入稳定阶段, 保持当前防控力度防止疫情反弹可能是下一阶段的重中之重。尽管如此, 现阶段的新增确诊病例数的环比增长率的波动过大, 结论存在较大不确定性, 相较累计确诊病例数的环比增长率, 由于其不稳定, 波动性较大, 建议应用环比增长率指标时针对累计确诊病例数进行分析。
借助累计确诊病例以及累计确诊病例数的环比增长率的一些指标, 从全国的空间约束聚类结果上看, 湖北及湖北周边的安徽、河南、湖南、江西等省份的累计确诊病例数较多, 环比增长率较大, 环比增长率的波动也较大, 下降趋势相对较弱, 说明防控效果相对差强人意, 复工复产需要谨慎对待。东部和南部省份的聚类累计确诊病例数的环比增长率都比较小, 且波动也相对较小, 说明疫情防控效果良好, 可以合理规划复工复产, 但也需要加强防控, 防止出现疫情反扑。北方省份和西北省份的一些聚类在确诊病例存量和环比增长上都相对乐观, 环比增长率的波动率存在一定差异, 但有可能是因为低基数导致, 这些地区可以考虑降低响应等级, 减少社会资源的消耗。黑龙江和吉林环比增长率较高, 说明近期该省份的防控措施需要得到加强, 防止疫情进一步扩散。
综上, 全国范围内疫情防控取得了初步成效, 全国疫情普遍出现增长放缓的趋势, 但局部地区的疫情风险仍然很高, 因此复工复产需要分区分级进行, 本研究基于疫情现状的空间约束聚类结果给分区管理提供科学依据。
-
图 1 我国2020年2月8日各省市的COVID-19累计确诊病例数分布图
Figure 1. Distribution of COVID-19 cumulative confirmed cases by provinces and cities in China in February 8, 2020
图 2 中国COVID-19累计确诊病例数的环比增长率曲线
Figure 2. Dod growth curve of COVID-19 cumulative confirmed cases in provinces and cities in mainland China
图 3 中国COVID-19新增确诊病例数的环比增长率曲线
Figure 3. Dod growth rate of COVID-19 newly confirmed cases in provinces and cities in mainland China
图 4 空间约束聚类中聚类数目与Calinski-Harabasz指数的关系图
Figure 4. Relationship between the number of clusters and the Calinski-Harabasz index in spatially constrained clustering
图 5 中国COVID-19空间聚类分布地图
Figure 5. Spatial clustering distribution map of COVID-19 in provinces and cities in mainland China
表 1 中国COVID-19累计确诊病例数的环比增长率的线性模型系数
Table 1. Linear model coefficients of the dod growth rate of COVID-19 cumulative confirmed cases in mainland China
省份 β1值 t值 P值 R2(%) 省份 β1值 t值 P值 R2(%) 吉林 -0.011 -1.017 0.328 7.37 辽宁 -0.022 -4.561 0.001 61.54 贵州 -0.016 -1.280 0.223 11.19 浙江 -0.040 -4.643 < 0.001 62.38 新疆 -0.033 -1.776 0.099 19.52 重庆 -0.021 -4.656 < 0.001 62.52 青海 -0.097 -2.103 0.057 26.94 安徽 -0.027 -4.789 < 0.001 63.82 内蒙古 -0.076 -2.368 0.034 30.13 河北 -0.041 -4.817 < 0.001 64.10 天津 -0.021 -2.627 0.021 34.67 江苏 -0.053 -4.848 < 0.001 64.38 海南 -0.034 -2.867 0.013 38.74 山东 -0.041 -5.170 < 0.001 67.28 河南 -0.057 -3.298 0.006 45.55 江西 -0.048 -5.575 < 0.001 70.51 湖南 -0.069 -3.330 0.005 46.03 云南 -0.069 -5.747 < 0.001 71.76 陕西 -0.075 -3.354 0.005 46.40 福建 -0.057 -5.803 < 0.001 72.15 湖北 -0.031 -3.544 0.004 49.14 四川 -0.034 -6.394 < 0.001 75.88 甘肃 -0.044 -3.610 0.003 50.06 广东 -0.025 -6.620 < 0.001 77.12 广西 -0.021 -4.081 0.001 56.16 山西 -0.032 -6.814 < 0.001 78.13 宁夏 -0.037 -4.156 0.001 57.05 北京 -0.020 -7.255 < 0.001 80.19 黑龙江 -0.027 -4.346 0.001 59.23 上海 -0.019 -7.594 < 0.001 81.60 
下载: 导出CSV
表 2 中国COVID-19新增确诊病例数的环比增长率的线性模型系数
Table 2. Linear model coefficients of the dod growth rate of COVID-19 newly confirmed casesin mainland China
省份 β1 t值 P值 R2(%) 省份 β1 t值 P值 R2(%) 甘肃 0.228 1.592 0.135 16.32 四川 -0.019 -1.007 0.332 7.24 黑龙江 0.076 1.133 0.278 8.98 上海 -0.023 -1.042 0.316 7.71 天津 0.054 0.544 0.596 2.22 山东 -0.021 -1.246 0.235 10.67 广西 0.015 0.323 0.752 0.80 浙江 -0.053 -1.572 0.140 15.98 吉林 0.016 0.176 0.863 0.28 陕西 -0.105 -1.721 0.109 18.56 辽宁 0.000 0.009 0.993 0.00 广东 -0.044 -1.737 0.106 18.84 山西 0.000 0.008 0.994 0.00 北京 -0.028 -1.739 0.106 18.88 贵州 -0.019 -0.270 0.792 0.60 宁夏 -0.136 -1.782 0.100 20.93 河北 -0.016 -0.368 0.719 1.03 河南 -0.043 -1.809 0.094 20.11 重庆 -0.012 -0.387 0.705 1.14 福建 -0.044 -1.847 0.088 20.79 内蒙古 -0.034 -0.416 0.684 1.31 湖北 -0.068 -1.849 0.087 20.83 新疆 -0.053 -0.418 0.682 1.33 江西 -0.044 -1.899 0.080 21.71 青海 -0.077 -0.593 0.572 4.78 湖南 -0.066 -1.995 0.067 23.43 海南 -0.030 -0.836 0.418 5.10 江苏 -0.038 -2.894 0.013 39.18 安徽 -0.041 -0.909 0.380 5.97 云南 -0.068 -3.142 0.008 43.16
下载: 导出CSV
表 3 中国COVID-19聚类结果
Table 3. COVID-19 clustering results of provinces and cities in China
聚类 省份 累计确诊病例数(个) 环比增长率 M值 S值 线性趋势系数 1 湖北省 27 100 0.23 0.20 -3.54 x值 27 100 0.23 0.20 -3.54 S2值 2 甘肃省 81 0.14 0.28 -3.61 宁夏回族自治区 45 0.11 0.22 -4.16 新疆维吾尔自治区 45 0.14 0.34 -1.78 x值 57 0.13 0.28 -3.18 S2值 17 0.02 0.05 1.02 3 内蒙古自治区 54 0.13 0.62 -2.37 陕西省 208 0.16 0.49 -3.35 x值 131 0.15 0.55 -2.86 S2值 77 0.02 0.06 0.49 4 北京市 326 0.17 0.10 -7.25 福建省 250 0.13 0.30 -5.80 广东省 1 120 0.17 0.13 -6.62 广西壮族自治区 195 0.12 0.13 -4.08 河北省 206 0.16 0.23 -4.82 江苏省 468 0.17 0.30 -4.85 辽宁省 105 0.09 0.12 -4.56 山东省 435 0.13 0.23 -5.17 山西省 115 0.18 0.16 -6.81 上海市 292 0.16 0.09 -7.59 四川省 386 0.12 0.17 -6.39 云南省 140 0.10 0.36 -5.75 浙江省 1 075 0.12 0.22 -4.64 重庆市 446 0.12 0.12 -4.66 x值 397 0.14 0.19 -5.64 S2值 309 0.03 0.08 1.08 5 天津市 88 0.09 0.16 -2.63 x值 88 0.09 0.16 -2.63 S2值 6 黑龙江省 307 0.23 0.16 -4.35 吉林省 78 0.21 0.17 -1.02 x值 193 0.22 0.17 -2.68 S2值 115 0.01 0.01 1.66 7 青海省 18 0.06 0.76 -1.64 x值 18 0.06 0.76 -1.64 S2值 8 安徽省 779 0.18 0.15 -4.79 贵州省 96 0.22 0.22 -1.28 河南省 1 033 0.19 0.38 -3.30 湖南省 838 0.17 0.46 -3.33 江西省 740 0.19 0.26 -5.58 x值 697 0.19 0.29 -3.65 S2值 317 0.02 0.11 1.47
下载: 导出CSV
-
[1] World Health Organization. Coronavirus disease(COVID-19)outbreak situation[EB/OL]. (2020-02-23)[2020-03-05]. https://www.who.int/emergencies/diseases/novel-coronavirus-2019. [2] 中国疾病预防控制中心.新型冠状病毒肺炎专栏[EB/OL]. (2020-02-23)[2020-03-07]. http://www.chinacdc.cn/jkzt/crb/zl/szkb_11803/.Chinese Center for Disease Control and Prevention. COVID-19 column[EB/OL]. http://www.chinacdc.cn/jkzt/crb/zl/szkb_11803/. [3] 中华人民共和国国家卫生健康委员会.新型冠状病毒肺炎疫情通报[EB/OL]. (2020-02-23)[2020-03-05]. http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml.National Health Commission of the people's Republic of China. COVID-19 notification[EB/OL]. (2020-02-23)[2020-03-05]. http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml. [4] 胡健, 胡艺, 高风华, 等.基于SKATER聚类算法设计血吸虫病监测点的探索性研究[J].中国血吸虫病防治杂志, 2019, 31(4): 368-373.DOI: 10.16250/j.32.1374.2019011.Hu J, Hu Y, Gao FH, et al. Design of schistosomiasis surveillance sites based on Spatial Kluster Analysis by Tree Edge Removal(SKATER)method: an exploratory study[J]. Chin J Schisto Control, 2019, 31(4): 368-373. DOI: 10.16250/j.32.1374.2019011. [5] Wu C, Hu W, Zhou MJ, et al. Data-driven regionalization for analyzing the spatiotemporal characteristics of air quality in China[J]. Atmos Environ, 2019, 203: 172-182.DOI: 10.1016/j.atmosenv.2019.01.048. [6] Openshaw S, Rao L. Algorithms for reengineering 1991 Census geography[J]. Environ Plan A, 1995, 27(3): 425-446.DOI: 10.1068/a270425. [7] Cockings S, Harfoot A, Martin D, et al. Maintaining existing zoning systems using automated zone-design techniques: methods for creating the 2011 census output geographies for England and Wales[J]. Environ Plan A, 2011, 43(10): 2399-2418.DOI: 10.1068/a43601. [8] Aarts EH, Van Laarhoven PJ.Pattern recognition theory and applications[M].Berlin: Springer, 1987: 179-192. [9] Caliński T, Harabasz J. A dendrite method for cluster analysis[J]. Commun Stat-Theory Methods, 1974, 3(1): 1-27.DOI: 10.1080/03610927408827101. [10] 中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组.新型冠状病毒肺炎流行病学特征分析[J].中华流行病学杂志, 2020, 41(2): 145-151.DOI: 10.3760/cma.j.issn.0254-6450.2020.02.003.Novel Coronavirus Pneumonia Emergency Response Epidemiology Team. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases(COVID-19)in China[J]. Chin J Epidemiol, 2020, 41(2): 145-151. DOI: 10.3760/cma.j.issn.0254-6450.2020.02.003. [11] Wu Z, McGoogan JM. Characteristics of and important lessons from the coronavirus disease 2019(COVID-19)outbreak in China: summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention[J]. JAMA, 2020.DOI: 10.1001/jama.2020.2648. [12] Du Z, Wang L, Cauchemez S, et al. Risk for transportation of 2019 novel coronavirus disease from Wuhan to other Cities in China[J]. Emerg Infect Dis, 2020, 26(5). http://www.researchgate.net/publication/338927327_Risk_for_Transportation_of_2019_Novel_Coronavirus_COVID-19_from_Wuhan_to_Cities_in_China 期刊类型引用(1)
1. 孙诚钰. 论突发公共卫生事件技术治理的行政法治因应. 河南社会科学. 2021(04): 9-16 . 
百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 488
- HTML全文浏览量: 193
- PDF下载量: 36
- 被引次数: 2