-
摘要:
目的 提出一种新的网络模型以解决COVID-19出现初期认知不够、检测能力受限以及潜伏期长等因素导致每天检测出的感染人数与真实感染人数存在差异的问题,并预测COVID-19疫情发展趋势。 方法 以历史时间窗检测出的数据为依据,将时间窗策略结合长短期记忆(long short term memory, LSTM)网络模型对世界各个地区的确诊人数进行预测分析。 结果 基于时间窗的LSTM网络模型与其他模型相比准确度较高。对时间窗宽度进行分析发现,当宽度取5时预测结果最接近真实数据,这与COVID-19的潜伏期普遍为3~7 d相吻合。 结论 该方法为COVID-19疫情发展以及其潜伏期的分析提供了参考。 Abstract:Objective To solve the data difference between COVID-19 confirmed cases and actual number of COVID-19 infections, a new model is proposed to predict the spread of the disease. The data difference has been mainly caused by insufficient understanding in the early stage of transmission, limited detection capabilities and the long incubation period. Methods The historical data of the number of confirmed cases are analyzed based on Window-Time. A Long Short-Term Memory (LSTM) network model is combined with the Window-Time strategy to analyze and predict the actual number of infections according to data published of various regions in the world. Results The LSTM network model with Window-Time strategy has higher accuracy than other models. Tuning the width of the Window-Time to the width of 5, the prediction result shows that it is closest to the real actual number of infections, which is consistent with the incubation period of COVID-19 generally known as 3-7 days. Conclusion This method provides a reference for the analysis of the transmission rate of COVID-19 and the incubation period of the epidemic. -
Key words:
- COVID-19 /
- Window-Time /
- LSTM network
-
本研究从流行病特征出发,利用时间窗策略处理的检测数据为分析依据,以当日前后时间段为采样检测数据范围,降低了仅依靠单日检测数据存在不准确性的风险。同时建立基于时间窗的长短期记忆(long short term memory, LSTM)网络模型对COVID-19的疫情传播规律进行分析,预测世界各地未来30 d内COVID-19感染人数。
1. 数据与方法
1.1 数据来源
搜集中国及世界各地共计252个国家、地区自疫情发生以来截至2020年11月20日每日累计的确诊、疑似、康复以及死亡人数的数据共65 027条,其中国内10 377条,国外54 650条[1],并对采集到的地区、日期数据进行数值化处理。
1.2 研究方法
1.2.1 时间窗策略
依据COVID-19的无症状感染性、检测隐藏性等特点,当日检测出的确诊数据并不能真实有效地体现出当日实际感染人数,因此提出时间窗数据采集策略,通过综合采用当日检测及其前后一段时间内的检测确诊数据,降低由潜伏期、检测能力等因素引起的确诊数据误差。
定义1。时间窗:采集某日疫情数据时考虑影响该数据的时间段。疫情数据采集日的数据由时间窗内疫情数据综合确定,通过分析该时间段内疫情检测数据,推测出采集日真实感染人数。
定义2。时间窗单向关联宽度:简称时间窗宽度,用字母n表示。对于d1、d2日,如果|d1-d2 |≤n,那么d1日与d2日疫情数据相关联。
定义3。时间窗双向关联影响系数:时间窗内的某天,用字母k表示。在时间窗单向关联宽度n内,k∈[-n, n]。
时间窗策略下某日疫情数据采集函数如式(1)所示。
$$ y\left( d \right) = \sum\limits_{\left( {d = d - n} \right)}^{\left( {d + n} \right)} {a{e^{ - |k|}}x} \left( d \right)\;\left( {k = 0, \pm 1, \pm 2, \ldots , \pm n} \right) $$ (1) 其中,x(d)表示d日的疫情检测数据,y(d)表示经过时间窗策略处理后d日的疫情数据,n为时间窗单向关联宽度,即d日的疫情数据与前后n天的每日疫情数据相关联。k为时间窗双向关联影响系数,ae-|k|表示d日前后k天的每日疫情数据对d日疫情数据的影响程度。假设随着前、后双向关联影响系数k绝对值的增大,其对当日数据的影响程度越小,文中影响程度采用指数分布衰减。
为确保时间窗采集数据与每日检测数据的量纲统一,对时间窗函数进行标准化处理,如式(2)所示。
$$ \sum\limits_{\left( {k = - n} \right)}^{\left( {k = n} \right)} {a{e^{ - |k|}}} = 1 $$ (2) 由公式(2)可以看出,当k∈[-n, 0]时,a的值呈指数递增;当k∈(0, n]时,a的值呈指数递减。即在时间窗内,距离当日的时间越长,其数据对当日数据的影响程度按指数分布减小。
1.2.2 基于时间窗的LSTM疫情分析模型
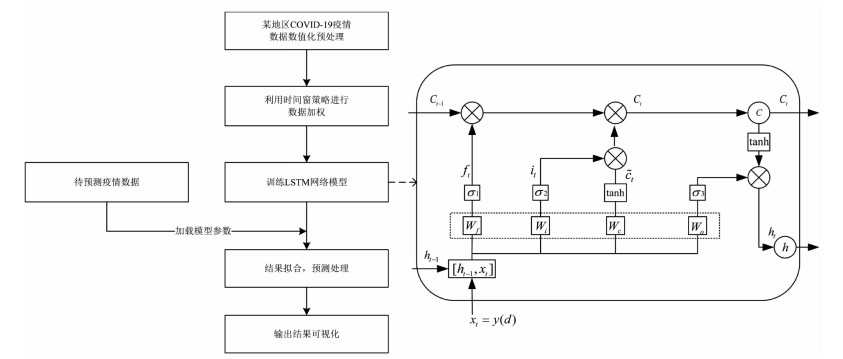
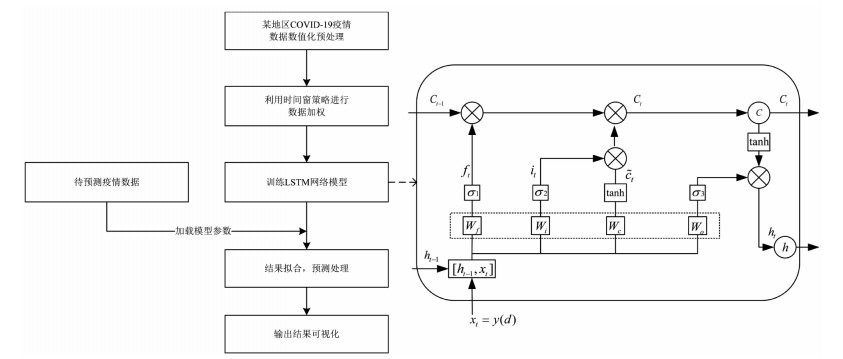
本研究面向COVID-19疫情分析的基于时间窗的LSTM网络模型如图 1所示,主要分为五个模块:①首先将采集到的数据转换为与LSTM网络模型输入一致的格式。②选择最佳的时间窗宽度,利用时间窗策略对每日确诊数据进行加权处理,降低由检测能力、潜伏期等因素导致的确诊数据误差。③将处理好的数据放入LSTM网络模型进行训练,其中隐含层LSTM包含输入门、遗忘门及输出门。④加载训练好的网络模型参数,输入待预测地区疫情数据预测之后30 d内该地区每日的确诊人数。⑤最后通过可视化操作对模型预测结果进行分析。
图 1右侧具体描述了LSTM单元结构。其中C(t-1)→Ct为LSTM单元状态的更新。首先,σ1通过查询h(t-1)和xt来决定是否丢弃某种信息,并得到遗忘门ft,如公式(3)所示。
$$ {f_t} = {\sigma _1}({W_f}\cdot[{h_{(t - 1)}}, {x_t}] + {b_f}) $$ (3) 为确定在网络中存储哪些信息,σ2通过查询h(t-1)和xt来决定是否存储某种信息,并得到输入门it,通过tanh层添加新的状态 $ {\tilde C}$t,如公式(4),(5)所示。
$$ {i_t} = {\sigma _2}\left( {{W_i}\cdot\left[ {{h_{(t - 1)}}, {x_t}} \right] + {b_i}} \right) $$ (4) $$ {{\tilde C}_t} = tanh({W_c} \cdot [{h_{(t - 1)}}, {x_t}] + {b_c}) $$ (5) 利用遗忘门ft与输入门it加权旧状态C(t-1)与新状态$ {\tilde C}$t,对单元状态Ct进行更新,如公式(6)所示。
$$ {C_t} = {f_t}\cdot{C_{(t - 1)}} + {i_t}\cdot{{\tilde C}_t} $$ (6) 最后,σ3通过查询h(t-1)和xt来决定是否输出哪些信息,并得到输出门Ot,通过tanh层设置单元状态置并对输出门Ot进行加权处理,如公式(7),(8)所示。
$$ {O_t} = {\sigma _3}({W_O}\cdot[{h_{(t - 1)}}, {x_t}] + {b_O}) $$ (7) $$ {h_t} = {O_t} \cdot tan{h_{({C_t})}} $$ (8) 其中σi,i=1,2,3为sigmoid激活函数,W和b分别为权重和偏置项,在训练过程中通过自适应矩估计(adaptive moment estimation, Adam)优化器更新,从而调整网络输出。
2. 结果
2.1 实验环境与参数
采用Tensorflow和Keras框架建立LSTM网络模型,LSTM输入层维度是三维,其中包含三个参数batch_size、input_dim和time_step,隐含层有一个参数n_hidden,输出层有两个参数n_hidden和output_dim。batch_size指一次性输入到神经网络中的样本数,设置为10时模型基本趋于稳定;时间步长time_step设置为3,即每个单元输出与前3个单元相关;input_dim即一次输入向量的维度,设置为6,分别为地区、日期、确诊、疑似、康复、死亡人数;n_hidden表示用于记忆和储存过去状态的节点个数,实验中设置为30;输出预测确诊人数结果维度output_dim设置为1。数据训练轮次epochs设置为100;模型预测天数设置为30;模型的损失函数loss采用均方误差(mean square error, MSE),其公式如式(9)所示;训练集与测试集的比例为9∶1。
$$ {\rm{MSE}} = 1/n\sum\nolimits_{(i = 1)}^n {|{x_i} - {{\hat x}_i}{|^2}} $$ (9) 2.2 模型评价指标
为检验模型预测结果并对所提模型进行公平地评估,遵循通用的评价指标,包括平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE),计算公式如式(10)、式(11)、式(12)所示。
$$ {\rm{MAE}} = 1/n\sum\nolimits_{(i = 1)}^n {|{x_i} - {{\hat x}_i}|} $$ (10) $$ {\rm{RMSE}} = \sqrt {1/n{{\sum\nolimits_{(i = 1)}^n {|{x_i} - {{\hat x}_i}|} }^2}} $$ (11) $$ {\rm{MAPE = }}100\% /n\sum\nolimits_{(i = 1)}^n {|\frac{{{x_i} - {{\hat x}_i}{|^2}}}{{{x_i}}}} $$ (12) 其中xi为每天实际确诊人数,$ {\hat x}$i为模型预测确诊人数,n为总天数。
2.3 实验结果
2.3.1 时间窗宽度分析
依据WHO指出的COVID-19潜伏期比季节性流感病毒潜伏期要长,普遍为3~7 d,一般情况下最长不超过14 d。分别讨论时间窗宽度参数分别为1~14时的COVID-19疫情传播特征,选取美国1月22日至11月20日的疫情数据,以不同的时间窗宽度对数据进行预处理,并将处理过的数据作为LSTM网络模型的输入,模型参数如2.1所述。依据上述2.2三个评价指标,分析模型预测的好坏,以获取时间窗的最佳宽度从而进行进一步的疫情分析。见表 1。
表 1 时间窗宽度分析结果Table 1. Window-Time width analysis results宽度参数(n) 时间窗双向关联权重系数(a) 模型平均(RMSE) 模型平均(MAE) 模型平均(MAPE) 1 0.576 116 8 834.264 7 368.893 1.676 2 0.498 397 10 038.900 7 654.034 1.223 3 0.474 832 7 589.277 5 705.968 1.242 4 0.466 715 6 258.321 4 588.270 1.235 5 0.463 798 5 595.714 3 549.351 1.132 6 0.462 734 6 304.506 4 992.106 1.278 7 0.462 343 6 407.598 4 274.729 1.330 8 0.462 201 6 553.170 4 122.248 1.344 9 0.462 147 7 103.133 4 366.778 3.371 10 0.462 128 7 503.113 4 666.238 1.346 11 0.462 121 6 901.131 4 432.232 1.226 12 0.462 118 6 812.243 5 889.700 2.279 13 0.462 117 6 193.711 3 773.097 2.274 14 0.462 116 6 070.431 3 927.931 2.013 根据表 1中三个评价指标,可以发现当时间窗宽度n取5时,模型预测效果最好,这与Lauer等[2]的调查研究得出的结论一致,即COVID-19潜伏期约为5 d。
2.3.2 模型对比
为检验LSTM模型性能,选用Logistic增长模型、多层感知器(multilayer perceptron, MLP)模型与LSTM模型作比较。Logistic增长模型是一种S型曲线模型,符合传染病模型中的SIR模型。MLP是一种采用误差反向传播优化算法(error back-propagation algorithm, BP)的前馈式人工神经网络,是当前运用最广泛的神经网络。
选取湖北省2019年12月1日至2020年10月21日的疫情检测数据作为LSTM模型、Logistic回归分析模型和MLP模型的输入,预测2020年10月22日至2020年11月20日的疫情数据。同时,依据2.3.1分析结果,选取时间窗宽度为5的时间窗策略对2019年12月1日至2020年10月21日的疫情数据进行加权预处理并作为LSTM与其他模型的输入进行预测。通过评价指标RMSE、MAE、MAPE衡量模型的好坏,模型对比结果见表 2。
表 2 模型对比结果Table 2. Comparison results of different models模型 RMSE MAE MAPE LSTM 475.839 308.708 0.244 Logistic 1 663.310 1 343.311 0.357 MLP 16 664.960 3 232.017 17.914 WT-LSTM 418.427 180.829 0.059 WT-Logistic 1 406.375 721.579 0.267 WT-MLP 14 541.510 2 243.632 15.321 从性能指标来看LSTM模型预测结果最好,Logistic回归分析模型预测结果稍差一些,而MLP模型预测结果较差。这说明LSTM模型能很好地模拟疫情传播的非线性、随机性,预测性能较好,并且由于LSTM模型自身的结构特点,能够很好地避免因时间序列过长导致的梯度消失和梯度爆炸等问题。
在对数据进行时间窗策略处理之后,各个模型的准确度都有不用程度的上升,其中基于时间窗的LSTM模型预测结果最好,这表明使用时间窗策略来预处理数据能够有效提升模型的预测性能。
2.3.3 国内外疫情预测
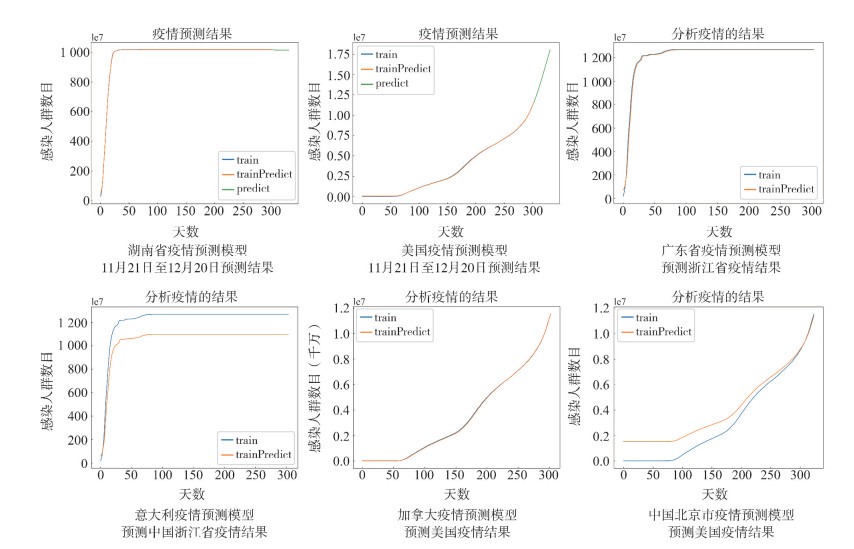
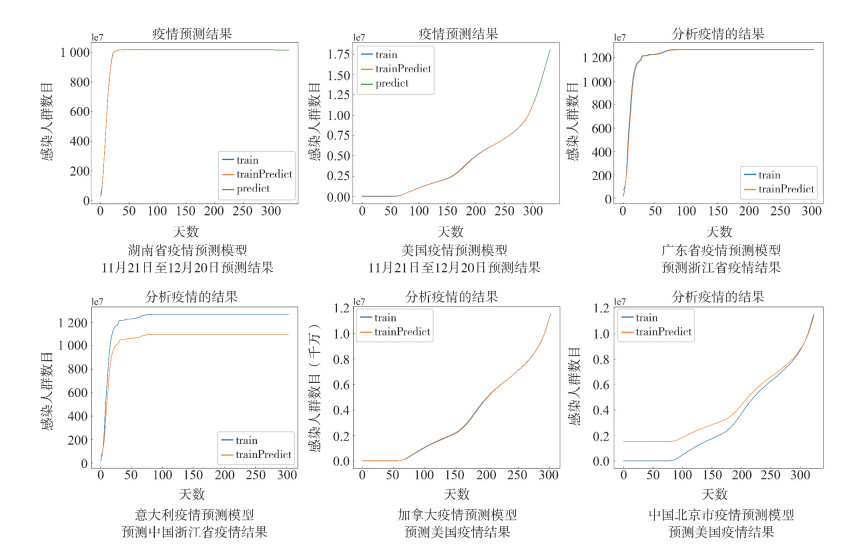
将中国各省市和世界各地的疫情数据分别利用时间窗宽度为5的时间窗策略进行加权预处理,依次将数据输入LSTM模型中,预测各地未来30 d的确诊人数。例如分别将湖南省2020年1月21日至10月21日、美国2020年1月22日至10月21日的疫情数据作为WT-LSTM模型的输入,训练模型并预测10月22日至11月20日的疫情确诊数据,同时与真实数据集进行对比。从结果可以看出,无论国内或者国外,WT-LSTM网络模型都能很好地拟合当地疫情数据。评价指标见表 3。
表 3 WT-LSTM网络模型预测实验评价指标Table 3. Evaluation index of experiments of WT-LSTM model模型 RMSE MAE MAPE 中国湖南省 6.271 2.160 0.001 美国 16 935.450 15 415.163 2.424 中国广东预测浙江 11.602 6.361 0.023 意大利预测浙江 93.185 89.672 0.283 加拿大预测美国 21 470.885 17 144.790 1.346 中国北京预测美国 644 572.900 567 618.440 271.889 在此基础上将湖南省、美国截止2020年11月20日的疫情数据放入WT-LSTM模型,预测未来30 d内的确诊数据。预测结果见图 2。结果显示湖南省疫情发生25 d左右,政府通过实施一系列防控措施使疫情达到了拐点。意大利和美国在11月20日之前疫情拐点尚未到来,预计确诊人数将持续上升,在2020年12月20日累计确诊人数将达到210万、1 800万。
2.3.4 国内外疫情对比分析
随机选取国内各省市及不同国家的疫情数据利用时间窗宽度为5的时间窗策略进行加权预处理并放入WT-LSTM模型中进行训练,再随机抽取另一地区疫情数据利用训练好的模型参数进行预测。例如分别利用广东省、意大利、加拿大、北京市的疫情数据训练WT-LSTM模型,再把浙江省、美国的疫情数据放入模型中,利用广东省与意大利训练好的模型预测浙江疫情确诊人数、加拿大和北京市训练好的模型预测美国确诊人数,以此作对比。可视化结果见图 2,评价指标见表 3。
由结果可知,国内之间和国外邻近国家之间的相互预测结果相对来说较为准确,而国外的预测模型在预测国内的疫情数据时,预测效果不佳,说明不同地区防疫政策的差异会导致感染人数增长趋势大相径庭。
3. 讨论
疫情预测通常以疾病出现以来每日检测出的被感染患者的人数为依据进行分析,然而COVID-19的特殊性导致检测出的数据与当日真实感染人数存在着差异,主要是由以下原因所致:①COVID-19作为人类历史上新的传染疾病,公众乃至科学家在其出现初期对其缺少深入了解,对其出现初期检测水平有限[3-5];②由于检测能力的限制,在暴发初期难以满足患者的检测需求;③COVID-19潜伏期大多为3~7 d,一般情况下最长不超过14 d,部分患者为无症状感染者,且潜伏期患者和无症状感染者具有传染性[2]。因而检测出的数据与当日实际感染人数存在差异,单纯以检测出的数据为依据进行COVID-19疫情预测将会给预测的准确性带来挑战。
根据国内外相关研究的发现,目前新冠传播研究大多基于传统的传染病数学模型,如易感-感染(susceptible-infected, SI)、易感-感染-恢复(susceptible-infected-recovered, SIR))和易感-暴露-感染-恢复(susceptible-exposed-infected-recovered, SEIR)模型等[6-7],这些模型使用微分方程的形式模拟流行病复杂的非线性模式,往往忽略了数据中的时间成分,也不能捕捉到传染病的传播动力学规律。也有诸多学者采用统计模型如滑动平均(moving average, MA)、自回归(autoregression, AR)及差分移动平均自回归(auto-regressive integrated moving average, ARIMA)[8],而这些模型参数绝大多数依赖于假设,这样假设的参数并不能完全拟合给定的数据,因此模型的精度较低。基于深度学习中循环神经网络模型(recurrent neural network, RNN)能够挖掘出数据中时序信息的特性,目前已有诸多学者将RNN模型用于研究传染病[9],然而传统的RNN模型在针对时间序列较长的问题进行建模训练时,回传的参数会随着回传次数的增加呈指数级下降。而LSTM网络模型通过输入门、遗忘门及输出门很好地解决了这个问题,适用于处理时间序列比较长的事件[10-11]。
COVID-19疫情数据本质上是动态的,若使用传统的统计和流行病学模型,结果往往是模糊的。因此具有记忆性的LSTM网络模型适用于研究COVID-19的传播规律。然而当前利用LSTM网络模型分析COVID-19的研究尚未考虑到由COVID-19特殊性所导致检测数据与真实感染人数的差异性,且大多数研究所采取的数据集较小,导致模型过拟合,预测结果不够精准[12-15]。鉴于上述问题,本研究设计一种时间窗策略,将其结合LSTM网络提出了基于时间窗的LSTM网络模型,并把大量疫情数据放入模型中,从而解决了检测数据与真实感染人数存在差异性的问题,提升了模型的准确度。
通过时间窗策略分析发现COVID-19的潜伏期约为5 d, 利用WT-LSTM网络模型进行国内外疫情预测及对比实验,发现中国通过有效的防控措施,令公众的防疫意识逐渐增强,当前中国疫情防控取得极大成效,新感染人数已显著减少。但在其他国家和地区,特别是美国、巴西、印度和欧洲,疫情形势依然严峻。因此, 每个国家和地区都需要采取有针对性的防控措施,才能有效控制疫情发展,防止疫情二次暴发。本研究将进一步参考最新的疫情数据,更新模型参数,提升模型预测性能。
-
表 1 时间窗宽度分析结果
Table 1. Window-Time width analysis results
宽度参数(n) 时间窗双向关联权重系数(a) 模型平均(RMSE) 模型平均(MAE) 模型平均(MAPE) 1 0.576 116 8 834.264 7 368.893 1.676 2 0.498 397 10 038.900 7 654.034 1.223 3 0.474 832 7 589.277 5 705.968 1.242 4 0.466 715 6 258.321 4 588.270 1.235 5 0.463 798 5 595.714 3 549.351 1.132 6 0.462 734 6 304.506 4 992.106 1.278 7 0.462 343 6 407.598 4 274.729 1.330 8 0.462 201 6 553.170 4 122.248 1.344 9 0.462 147 7 103.133 4 366.778 3.371 10 0.462 128 7 503.113 4 666.238 1.346 11 0.462 121 6 901.131 4 432.232 1.226 12 0.462 118 6 812.243 5 889.700 2.279 13 0.462 117 6 193.711 3 773.097 2.274 14 0.462 116 6 070.431 3 927.931 2.013 表 2 模型对比结果
Table 2. Comparison results of different models
模型 RMSE MAE MAPE LSTM 475.839 308.708 0.244 Logistic 1 663.310 1 343.311 0.357 MLP 16 664.960 3 232.017 17.914 WT-LSTM 418.427 180.829 0.059 WT-Logistic 1 406.375 721.579 0.267 WT-MLP 14 541.510 2 243.632 15.321 表 3 WT-LSTM网络模型预测实验评价指标
Table 3. Evaluation index of experiments of WT-LSTM model
模型 RMSE MAE MAPE 中国湖南省 6.271 2.160 0.001 美国 16 935.450 15 415.163 2.424 中国广东预测浙江 11.602 6.361 0.023 意大利预测浙江 93.185 89.672 0.283 加拿大预测美国 21 470.885 17 144.790 1.346 中国北京预测美国 644 572.900 567 618.440 271.889 -
[1] World Health Organization. Coronavirus Disease (COVID-19)[EB/OL]. (2020-11-20)[2020-11-20]. https://www.who.int/emergencies/diseases/novel-coronavirus-2019 [2] Lauer SA, Grantz KH, Bi Q, et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application[J]. Ann Intern Med, 2020, 172(9): 577-582. DOI: 10.7326/M20-0504. [3] Sohrabi C, Alsafi Z, O'Neill N, et al. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19)[J]. Int J Surg, 2020, 76: 71-76. DOI: 10.1016/j.ijsu.2020.02.034. [4] Huang C, Wang Y, Li X, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China[J]. Lancet, 2020, 395(10223): 497-506. DOI: 10.1016/S0140-6736(20)30183-5. [5] Ying S, Li F, Geng X, et al. Spread and control of COVID-19 in China and their associations with population movement, public health emergency measures, and medical resources[J]. medRxiv, 2020, 2020.02.24.20027623. DOI: 10.1101/2020.02.24.20027623. [6] Li MY, Muldowney JS. Global stability for the SEIR model in epidemiology[J]. Math Biosci, 1995, 125(2): 155-164. DOI: 10.1016/0025-5564(95)92756-5. [7] 梅文娟, 刘震, 朱静怡, 等. 新冠肺炎疫情极限IR实时预测模型[J]. 电子科技大学学报, 2020, 49(3): 362-368. DOI: 10.12178/1001-0548.2020063.Mei WJ, Liu Z, Zhu JY, et al. Extreme IR model for COVID-19 real-time forecasting[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(3): 362-368. DOI: 10.12178/1001-0548.2020063. [8] Chintalapudi N, Battineni G, Amenta F. COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: A data driven model approach[J]. J Microbiol Immunol Infect, 2020, 53(3): 396-403. DOI: 10.1016/j.jmii.2020.04.004. [9] Yin R, Zhang Y, Zhou X, et al. Time series computational prediction of vaccines for influenza A H3N2 with recurrent neural networks[J]. J Bioinform Comput Biol, 2020, 18(1): 2040002. DOI: 10.1142/S0219720020400028. [10] 王淑平, 杜敏, 罗建伟, 等. GM(1, 1)模型与LSTM神经网络在肺结核发病数预测中的应用[J]. 公共卫生与预防医学, 2019, 30(5): 11-14. doi: 10.3969/j.issn.1006-2483.2019.05.003Wang SP, Du M, Luo JW, et al. Application of GM(1, 1) model and LSTM neural network in predicting the incidence of pulmonary tuberculosis[J]. J of Pub Health and Prev Med, 2019, 30(5): 11-14. DOI: 10.3969/j.issn.1006-2483.2019.05.003. [11] 高秋菊, 周宇畅, 赵树青, 等. ARIMA乘积季节模型和LSTM深度神经网络对石家庄市手足口病疫情预测效果的比较[J]. 中华疾病控制杂志, 2020, 24(1): 73-78. DOI: 10.16462/j.cnki.zhjbkz.2020.01.015.Gao QJ, Zhou YC, Zhao SQ, et al. Comparison on predictive capacity of ARIMA model and LSTM model for incidence of hand, foot and mouth disease in Shijiazhuang[J]. Chin J Dis Control Prev, 2020, 24(1): 73-78. DOI: 10.16462/j.cnki.zhjbkz.2020.01.015. [12] Yang Z, Zeng Z, Wang K, et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions[J]. J Thorac Dis, 2020, 12(3): 165-174. DOI: 10.21037/jtd.2020.02.64. [13] Tomar A, Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures[J]. Sci Total Environ, 2020, 728: 138762. DOI: 10.1016/j.scitotenv.2020.138762. [14] Chimmula VKR, Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks[J]. Chaos Solitons Fractals, 2020, 135: 109864. DOI: 10.1016/j.chaos.2020.109864. [15] Chatterjee A, Gerdes MW, Martinez SG. Statistical explorations and univariate timeseries analysis on COVID-19 datasets to understand the trend of disease spreading and death[J]. Sensors (Basel), 2020, 20(11): 3089. DOI: 10.3390/s20113089. 期刊类型引用(1)
1. 许晓萌,崔世恒,王亚菲,孙丽,丛艳丽,王晶辉,李静,张振国. 长短时记忆神经网络模型在河北省麻疹疫情发病趋势预测中应用. 中国公共卫生. 2023(11): 1464-1468 .  百度学术
百度学术其他类型引用(5)
-
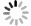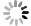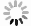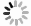





 下载:
下载:

 下载:
下载: