Comparison of propensity score matching with mixed-effect model in cluster randomized trial
-
摘要:
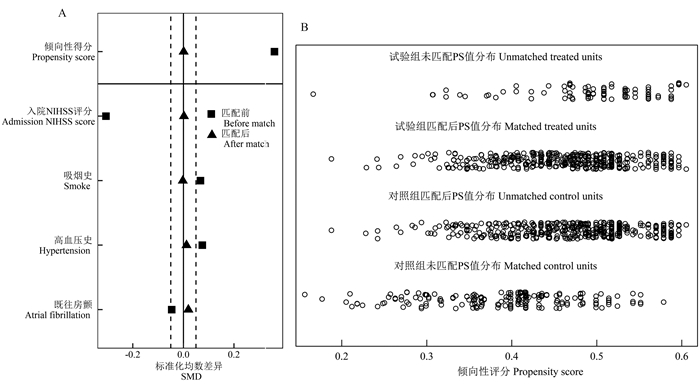
目的 比较倾向性评分匹配(propensity score matching, PSM)法和混合效应模型法在群随机试验中的统计效能,为同类研究的统计分析方法选择提供指导。 方法 通过模拟研究与急性缺血性脑卒中疗效评级数据,比较倾向性评分后拟合单因素条件logistic回归分析模型和直接拟合混合效应模型应用于含有混杂因素的群随机试验数据时的统计学性能,说明方法应用场景和选择策略。 结果 PSM后,各混杂因素组间均衡性明显改善。条件logistic回归分析模型和混合效应模型处理效应估计结果十分接近,但前者的P值更小。实例分析结果显示,匹配后各混杂因素的标准化均数差异(standardized mean difference, SMD)均控制在0.1以内,条件logistic回归分析模型识别出两个研究结局的处理组间差异;而混合效应模型仅识别出7 d有效率的处理组间差异。 结论 PSM可以平衡群随机试验中的混杂因素,提高两组间的可比性,其检验效能较高。推荐在临床群随机试验中优先考虑PSM法,但也要注意其应用条件和局限性。 Abstract:Objective To compare the efficacy of propensity score matching (PSM) and mixed-effect model in statistical performance, providing methodological guidance for similar studies. Methods Employing a simulation study and a case study of acute ischemic stroke, this research compared the statistical performance of propensity score matching followed by univariate conditional logistic regression and mixed-effect model. It aims to illustrate their application scenarios and selection strategies in cluster randomized data involving confounders. Results In the simulation study, the balance of confounders between groups was significantly improved after PSM. Conditional logistic model provides similar treatment effect estimates but smaller P values compared with mixed-effect model. In the acute ischemic stroke case study, the standardized mean difference (SMD) of confounders were reduced below 0.1 after matching. Conditional logistic model identified the between-group difference in both outcomes. In contrast, mixed-effect model only identified the between-group difference in 7-day effective rate. Conclusions Propensity score matching can effectively improves groups comparability. Compared with mixed-effect model, conditional logistic model based on matched data has higher power of test. PSM is advisable for priority consideration in clinical cluster randomized trials, keeping in mind its specific application conditions and limitations. -
Key words:
- Cluster randomized trials /
- Propensity score /
- Mixed-effect model
-
表 1 模拟数据混杂变量分布
Table 1. Sampling distribution of confounding in the simulated data
混杂效应Mixed effect 分组Group X1 X2 X3 低差异Low difference 对照组Control N(0.0, 1.0) N(0.0, 4.0) Bernouli(0.45) 试验组Treatment N(0.3, 1.0) N(0.6, 4.0) Bernouli(0.30) 高差异High difference 对照组Control N(0.0, 1.0) N(0.0, 4.0) Bernouli(0.60) 试验组Treatment N(0.6, 1.0) N(1.2, 4.0) Bernouli(0.30) 表 2 两种方法疗效指标分析
Table 2. Analysis of efficacy indicators of different methods
结局指标
Outcome方法
Method试验组发生人数(占比/%)
Number of occurrences in treatment group(proportion/%)对照组发生人数(占比/%)
Number of occurrencesin control group(proportion/%)OR值value
(95% CI)P值
valueNIHSS 7 d有效率
7-day NIHSS effective rate混合效应模型
Mixed-effect model372(73.96) 405(67.73) 1.404(1.074~1.836) 0.013 PSM后条件logistic回归分析模型
Conditional logistic model321(75.89) 282(66.67) 1.574(1.164~2.128) 0.003 90 d mRS评分≤2分
90-day mRS score≤2 score混合效应模型
Mixed-effect model381(78.56) 377(66.73) 1.459(0.939~2.265) 0.093 PSM后条件logistic回归分析模型
Conditional logistic model311(76.98) 285(70.54) 1.513(1.073~2.132) 0.018 -
[1] 黄丽红, 王永吉, 王素珍, 等. 倾向性评分方法及其规范化应用的统计学共识[J]. 中国卫生统计, 2020, 37(6): 952-958. DOI: 10.3969/j.issn.1002-3674.2020.06.041.Huang LH, Wang YJ, Wang SZ, et al. Statistical consensus on peopensity score methods and their normative application[J]. Chinese Journal of Health Statistics, 2020, 37(6): 952-958. DOI: 10.3969/j.issn.1002-3674.2020.06.041. [2] Lalani N, Jimenez RR, Yeap B. Understanding Propensity Score Analyses[J]. Int J Radiat Oncol, 2020, 107(3): 404-407. DOI: 10.1016/j.ijrobp.2020.02.638. [3] 龚清海, 张晓宏, 徐琛玮. 混合效应模型在系统分组资料中的应用及SAS实现[J]. 中国卫生统计, 2009, 26(6): 577-579. DOI: 10.3969/j.issn.1002-3674.2009.06.005.Gong QH, Zhang XH, Xu CW. Mixed model in the hierarchical classification datas and implementation of SAS[J]. Chinese Journal of Health Statistics, 2009, 26(6): 577-579. DOI: 10.3969/j.issn.1002-3674.2009.06.005. [4] Austin PC. Optimal caliper widths for propensity-score matching when estimating differences in means and differences in proportions in observational studies[J]. Pharmaceutical Statistics, 2011, 10(2): 150-161 DOI: 10.1002/pst.433. [5] Zhang XT, Zhong WS, Ma XD, et al. Ginkgolide with intravenous alteplase thrombolysis in acute ischemic stroke improving neurological gunction: a multicenter, cluster-randomized trial (GIANT)[J]. Front Pharmacol, 2021, 12: 792136-792134. DOI: 10.3389/fphar.2021.792136. [6] Benedetto U, Head SJ, Angelini GD, et al. Statistical primer: propensity score matching and its alternatives[J]. Eur J Cardiothorac Surg, 2018, 53(6): 1112-1117. DOI: 10.1093/ejcts/ezy167. [7] Zhang ZN. Propensity score method: a non-parametric technique to reduce model dependence[J]. Ann Transl Med, 2017, 5(1): 7-14. DOI: 10.21037/atm.2016.08.57. -




 下载:
下载: